Test: Digital Circuits & Flip Flops - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test - Test: Digital Circuits & Flip Flops
A logic network has two data inputs A and B, and two control inputs C0 and C1. It implements the function F according to the following table.
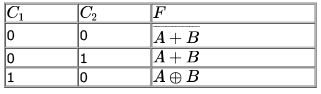
Implement the circuit using one 4 to 1 Multiplexer, one 2-input Exclusive OR gate, one 2-input AND gate, one 2-input OR gate and one Inverter.
In the following truth table, V = 1 if and only if the input is valid.

What function does the truth table represent?
Consider the following combinational function block involving four Boolean variables x,y,a,b where x,a,b are inputs and y is the output.
if(x, a,b,y)
{
if( x is 1) y=a;
else y=b;
}
Which one of the following digital logic blocks is the most suitable for implementing this function?
How many pulses are needed to change the contents of a 8-bit up counter from 10101100 to 00100111 (rightmost bit is the LSB)?
The minimum number of D flip-flops needed to design a mod-258 counter is
Let = k = 2n. A circuit is built by giving the output of an n-bit binary counter as input to an n- to-2n bit decoder. This circuit is equivalent to a
Consider a 4-bit Johnson counter with an initial value of 0000. The counting sequence of this counter is
The next state table of a 2-bit saturating up-counter is given below.
The counter is built as a synchronous sequential circuit using T flip-flops. The expressions for are
The dual of a Boolean function written as
is the same expression as that of F with + and swapped. F is said to be self-dual if
. The number of self-dual functions with Boolean variables is
Latches constructed with NOR and NAND gates tend to remain in the latched condition due to which configuration feature?
Find the maximum clock frequency at which the counter in the figure below can be operated. Assume that the propagation delay through each flip flop and each AND gate is 10 ns. Also assume that the setup time for the J K inputs of the flip flops is negligible.
The exponent of a floating-point number is represented in excess-N code so that:
The following is a scheme for floating point number representation using 16 bits
Let s, e, and m be the numbers represented in binary in the sign, exponent, and mantissa fields respectively. Then the floating point number represented is:
What is the maximum difference between two successive real numbers representable in this system?
Consider the following floating-point format.
Mantissa is a pure fraction in sign-magnitude form.
The decimal number has the following hexadecimal representation (without normalization and rounding off):
Consider the following floating-point format.
Mantissa is a pure fraction in sign-magnitude form.
The normalized representation for the above format is specified as follows. The mantissa has an implicit 1 preceding the binary (radix) point. Assume that only 0’s are padded in while shifting a field.
The normalized representation of the above number



















