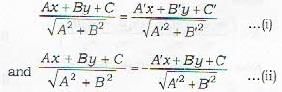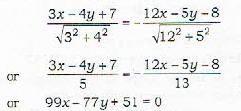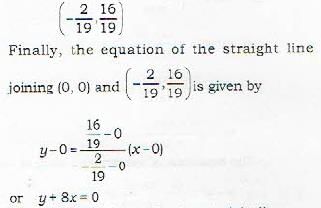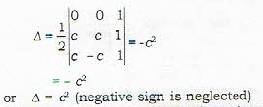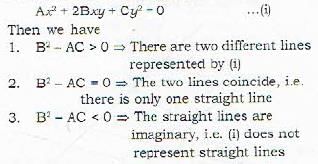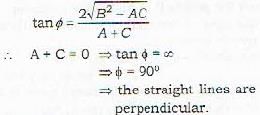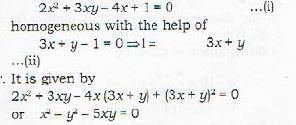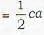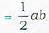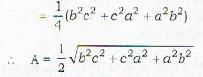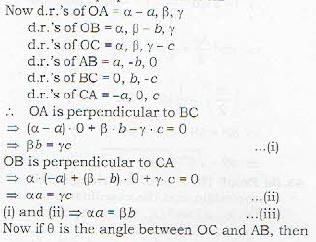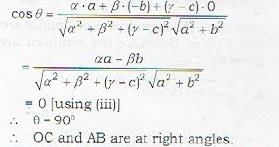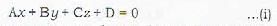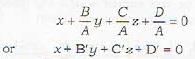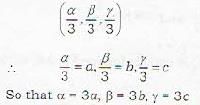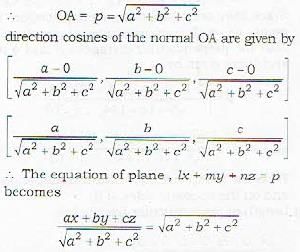Test: Dimensional Geometry - 5 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Dimensional Geometry - 5
The equation of the bisector of the angle between the lines 3x - 4y + 7 = 0 and 12x - 3y -8 =0 , in w hich the origin lines, is given by
The line joining the origin to the point of intersection of 2x + 5y- 4 = 0 and 3x-2y+ 2 = 0 is given by
The area of the triangle formed by the lines y -x = 0, y + x = 0, x - c = 0 is given by
The angle between the straight lines represented by the equation Ax2 + 2Bxy + Cy2 = 0 is given by
The lines represented by the equation Ax2 + 2Bxy + Cy2 = 0 are real, coincident or imaginary according as B2 - AC is
The lines represented by the equation Ax2 + 2Bxy + Cy2 = 0 are perpendicular if
The general equation of second degree ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 may represent a pair of straight lines if
The lines joining ihe origin to the points of intersection of 2x2 + 3xy - 4x + 1 = 0 and 3x + y - 1 = 0 are given by
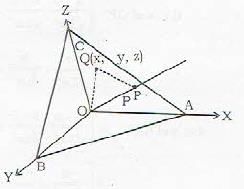
The area of the triangle ABC formed by the intercepts OA a, OB = h, OC = con the coordinate axes respectively by a plane is given by
If two pairs of opposite edges of a tetrahedron art; at right angles, then the third pair
If the pairs of opposite edges of a tetrahedron OABC are at right angles, then
How many arbitrary constants are there in the equation of a plane?
The equation of which of the following degree in x, y, z represents a plane
Which one of the following is the equation of the plane which meets the coordinale axes in A,B,C such that the centroid of the triangle ARC is (a,b,c)?
If l, m, n are the direction of the normal to the plane and p be the perpendicular distance from the origin on it, then the equation of the plane is of the type
The equation of the plane passing through the point A(a, b, c) and perpendicular to OA (O being origin) is given by
The equation of the plane passing through (2, -3, 1) and perpendicular to the line joining the points (3, 4. -1) and (2, -1, 5) is given by
The equation of the plane through the points (2, 3, 1) and (-4. 5. 3) and parallel to X - axis is given by
|
27 docs|150 tests
|