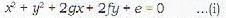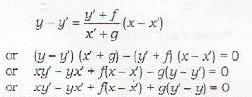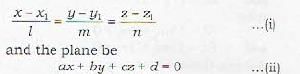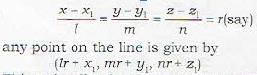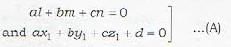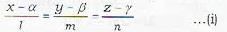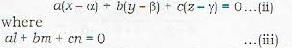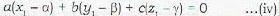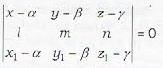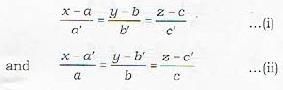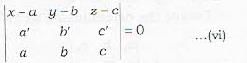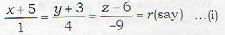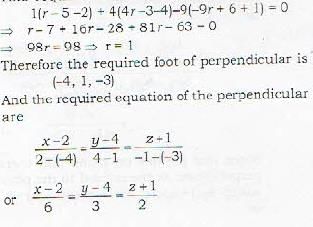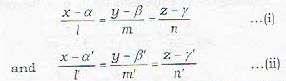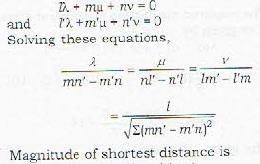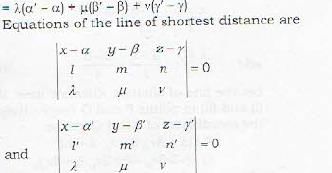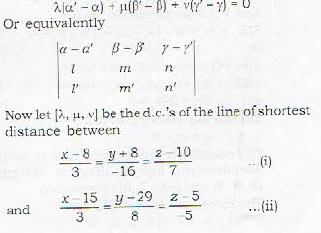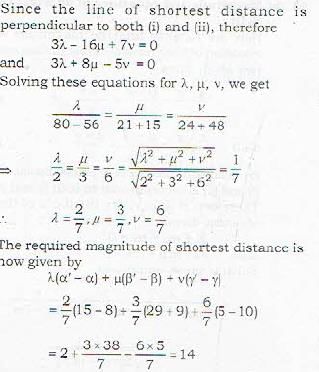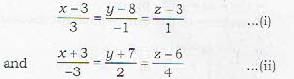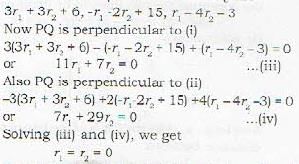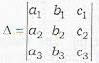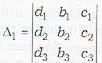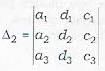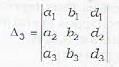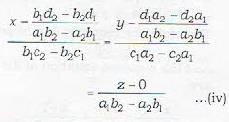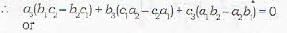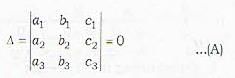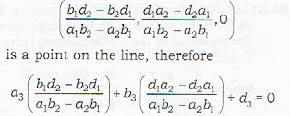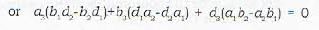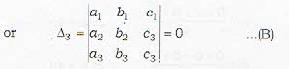Test: Dimensional Geometry - 9 - Mathematics MCQ
20 Questions MCQ Test - Test: Dimensional Geometry - 9
The equation of one of the tangents to the circle x2+y2 -6x+4y= 12 parallel to tlie straight line 4x+3y+5 = 0, is given by
The equation of the normal at point (x', y') of the circle x2+ y2+ 2gx + 2fy + c = 0 is given by
From any given point outside the circle, how many tangents can be drawn to a circle?
The pole of a given line Ax + By + C = 0 with respect to the circle x2 + y2 = a2, is given by
The pole of the straight line 9x + y = 28 with 2x2 + 2y2 -3x + 5x - 7 = 0 is the point whose coordinates are
The coordinates of the point, from which the lengths of the tangents to the circles
x2+ y2- 16x + 60 = 0
3x2 + 3y2 - 36x +81=0
x2 + y2- 16x- 12y + 84 = 0
are equal, are given by
The length of the tangent drawn from the point (6 , - 7) to the circle 3x2 + 3y2 - 7x - 6y-12 = 0 is given by
If (R, α) is the centre of the circle in terms of polar coordinates and a be its radius, then the polar equation of such circle is given by
Which of the following is/are the condition(s) that the line 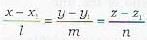 may lie in the plane ax + by - cz + d = 0, if
may lie in the plane ax + by - cz + d = 0, if
Which of the following lines lies in the plane x + 2y - 3z = 6?
The equation of the plane passing through the point (x1, y1, z1) and through the line 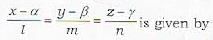
The equation of the plane containing the lines 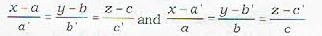 is not given by
is not given by
How many arbitrary constants occur in the equation of a straight line in general?
The equation of the perpendicular drawn from the point (2, 4, -1) to the line 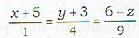 are given b
are given b
What is the magnitude of the line of shortest distance between the lines 
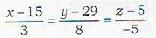
The equation of the line of shortest distance between the lines 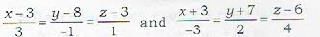 is given by
is given by
Which is a wrong statement? The three planes
a1x + b1y + c1z + d1 = 0
a2x + b2y + c2z + d2 = 0
a3x + b3y + c3z + d3 = 0
have a common line of intersection, if
Consider the three planes represented by
a1x + b1y + c1z + d1 = 0
a2x + b2y + c2z + d2 = 0
a3x + b3y + c3z + d3 = 0
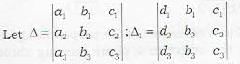
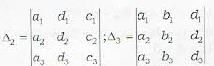
then the three planes will form a triangular prism if