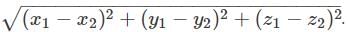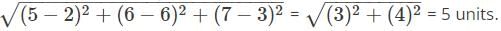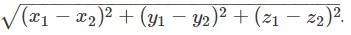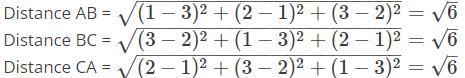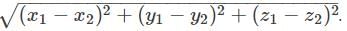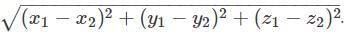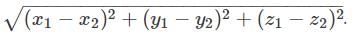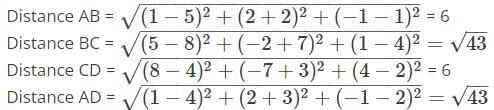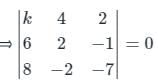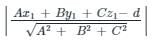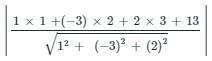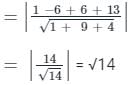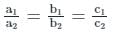Test: Distance between two points in 3D Space - SAT MCQ

We know, distance between two points (x₁, y₁, z₁) and (x₂, y₂, z₂) is 
So, distance between two points (5, 6, 7) and (2, 6, 3) will be 

We know, distance between two points (x₁, y₁, z₁) and (x₂, y₂, z₂) is 

Since AB = BC = CA so, it forms equilateral triangle.

We know, distance between two points (x₁, y₁, z₁) and (x₂, y₂, z₂) is 

Since AB = BC and AB²+BC² = AC² so, it forms right angled isosceles triangle.

We know, distance between two points (x₁, y₁, z₁) and (x₂, y₂, z₂) is 

Since AB = BC so, it forms isosceles triangle.

We know, distance between two points (x₁, y₁, z₁) and (x₂, y₂, z₂) is

Since AB = CD and BC = AD i.e. opposite two sides are equal so, it is a parallelogram.

Given:
The plane which passes through the point (5, 2, -4)
Plane is perpendicular to the line with direction ratios 2, 3, -1

Concept:
Cartesian equation of the plane passing through (x₁ , y₁ , z₁) and perpendicular to line having drs a, b, c is given by :
a(x - x₁) + b(y - y₁) + c(z - z₁) = 0

Solution:
Equation of plane :
2(x - 5) + 3(y - 2) -(z - (-4)) = 0
⇒ 2x + 3y - z = 20

CONCEPT:
If the points (x₁, y₁, z₁), (x₂, y₂, z₂) and (x₃, y₃, z₃) be collinear then 

CALCULATION:
 Given: The points (k, 4, 2), (6, 2, - 1) and (8, - 2, - 7) are collinear
As we know that, if the points (x₁, y₁, z₁), (x₂, y₂, z₂) and (x₃, y₃, z₃) be collinear then 

Here, x₁ = k, y₁ = 4, z₁ = 2, x₂ = 6, y₂ = 2, z₂ = - 1, x₃ = 8, y₃ = - 2 and z₃ = - 7

⇒ k × (- 14 - 2) - 4 × (- 42 + 8) + 2 × (- 12 - 16) = 0
⇒ - 16k + 136 - 56 = 0
⇒ 16k = 80
⇒ k = 5
Hence, option D is the correct answer.

Concept:

Perpendicular Distance of a Point from a Plane 

Let us consider a plane given by the Cartesian equation, Ax + By + Cz = d

And a point whose coordinate is, (x₁, y₁, z₁)

Now, distance = 
Calculation:

We have to find the distance of the point (1, 2, 3) form the plane x – 3y + 2z + 13 = 0

Distance =  

Concept:
Let two lines having direction ratios a₁, b₁, c₁, and a₂, b₂, c₂ respectively.
Condition for perpendicular lines: a₁a₂ + b₁b₂ + c₁c₂ = 0
Condition for parallel lines: 
 

Calculation:
Given lines are 
 
The direction ratio of the first line is (2k, 3, -1) and the direction ratio of second line is (8, 6, -2)
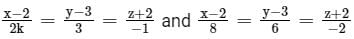Lines are parallel;

Concept:
The direction cosines of the vector are the cosines of angles that the vector forms with the coordinate axes.
Calculation:
Z-axis makes an angle 90° with X-axis, 90° with Y-axis, and 0° with Z-axis
∴ Direction cosines of Z-axis: cos 90, cos 90, cos 0
i.e., 0, 0, 1
Now sum of the direction cosine of z-axis = 0 +  0 + 1 = 1
Hence, option (3) is correct.