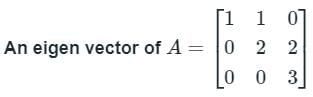Test: Eigenvalues & Eigenvectors - 1 - Electrical Engineering (EE) MCQ
20 Questions MCQ Test - Test: Eigenvalues & Eigenvectors - 1
Find the sum of the Eigenvalues of the matrix
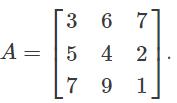
All the four entries of the 2 × 2 matrix  are nonzero, and one of its eigen values is zero. Which of the following statements is true?
are nonzero, and one of its eigen values is zero. Which of the following statements is true?
The three characteristic roots of the following matrix A
The sum of the eigenvalues of the matrix given below is
Eigen values of a matrix are 5 and 1. What are the eigen values of the matrix S2 = SS?
The number of linearly independent eigenvectors of
The eigenvectors of the matrix are written in the form
. What is a + b?
One of the Eigenvectors of the matrix A = 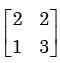 is
is
The minimum and the maximum eigen values of the matrix are –2 and 6, respectively. What is the other eigen value?
The state variable description of a linear autonomous system is, X= AX,
Where X is the two dimensional state vector and A is the system matrix given by
The roots of the characteristic equation are
For the matrix s one of the eigen values is equal to -2. Which of the following is an eigen vector?
x=[x1x2…..xn]T is an n-tuple nonzero vector. The n×n matrix V=xxT
Let A be an n x n complex matrix. Assume that A is self-adjoint and let B denotes the inverse of (A + iIn). Then all eigenvalues of (A - iIn)B are
If the rank of a (5×6) matrix Q is 4, then which one of the following statements is correct?
The trace and determinate of a 2 ×2 matrix are known to be – 2 and – 35 respectively. Its eigenvalues are
In matrix equation [A]{X} = {R}, one of the eigenvalues of matrix A is
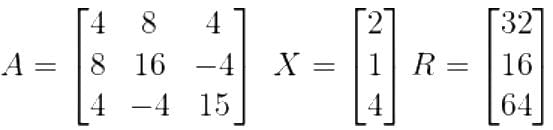


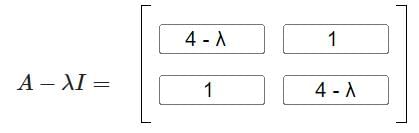
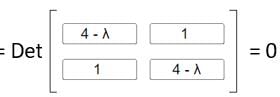




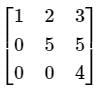 is
is