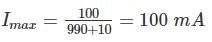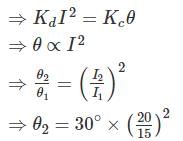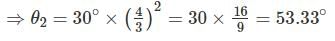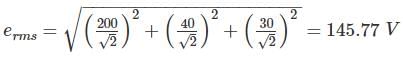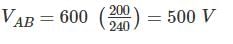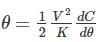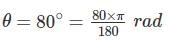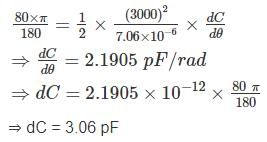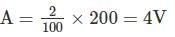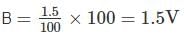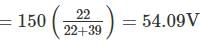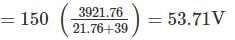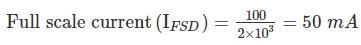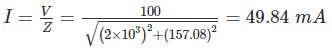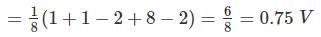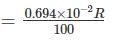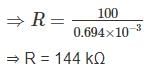Test: Electrical & Electronic Measurements- 2 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Electrical & Electronic Measurements- 2
An ideal diode has been connected across a 10 Ω, 100 mA, center-zero PMMC meter as shown in figure.
The meter will read
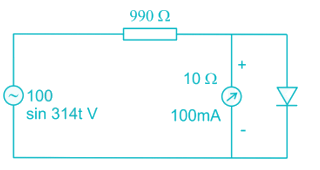
The meter will read

The deflecting torques of an ammeter varies as the square of the current passing through it. If a current of 15A produces a deflection of 30°, The deflection of a current of 20 A when instrument is spring controlled will be _____________ (in degrees).
A moving iron instrument has 10 Ω resistance and gives full scale deflection when carrying 50 mA. It can be used measure 750 V by using what resistance?
What will be the reading (in V) when a voltage e = 200 sin ωt + 40 sin (3ωt + 30°) + 30 cos (5 ωt + 21.5°) v is applied to an electrodynamometer voltmeter.
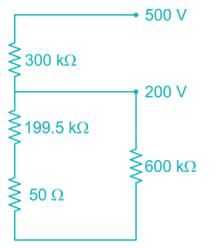
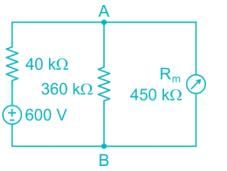
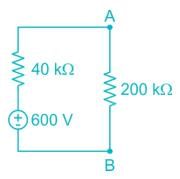
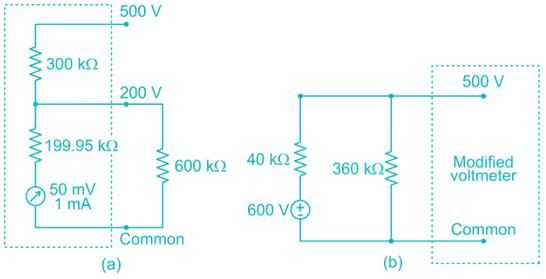
A 600 kΩ resistor is connected from the 200 V terminal to the common terminal of a dual scale voltmeter, as shown in figure (a). This modified voltmeter is then used to measure the voltage across the 360 kΩ resistor in the circuit in figure (b). What is the reading on the 500 V scale of the meter?
The spring constant of a 3000 V electrostatic voltmeter is 7.06 × 10-6 Nm/rad. The full scale deflection of the instrument is 80°. Assuming the rate of change of capacitance with angular deflection to be constant over the operating range. Calculate the total change of capacitance (in pF) from zero to full scale.
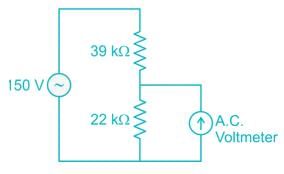
Two different a.c, voltmeters are used to measure the voltage across the 22 kΩ resister shown in figure. Meter A has a.c. sensitivity of 10 kΩ/V, a guaranteed accuracy of 98% at full scale, and is set on its 200V scale. Meter B has an a.c. sensitivity of 4kΩ/V. a guaranteed accuracy of 98.5% at full scale, and is set on its (0-100)V range. Which meter Provides more accurate results?
A moving iron instrument is calibrated with full scale deflection on 100 V DC. This instrument is used to measure 100 V at 50 Hz supply. Find the percentage error in reading if the instrument has a resistance of 2 kΩ and an inductance of 0.5 H
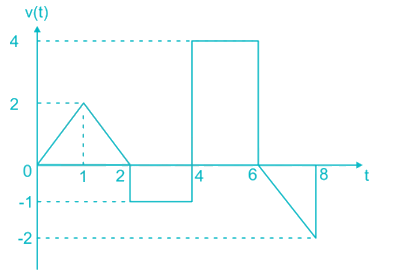
An input voltage represented by wave from as shown below is applied to a PMMC instrument. The reading of the instrument will be __ ( in V)
The coil of a moving coil voltmeter is 50 mm long and 40 mm wide and has 120 turns on it. The control spring exerts a torque 200 × 10-6 n – m when the deflection is 100 divisions on full scale. If the flux density of the magnetic field in the air gap is 1.2 wb/m2. The resistance that must be put in series with the coil to give one volt per division.