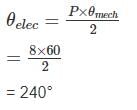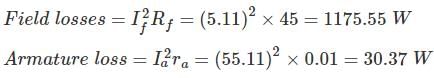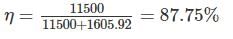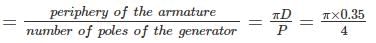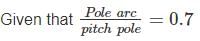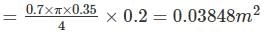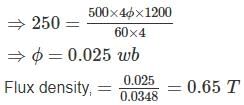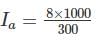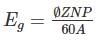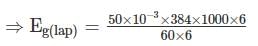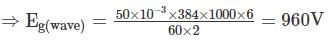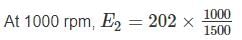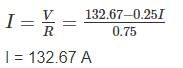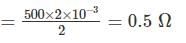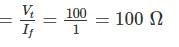Test: Electrical Machines- 3
10 Questions MCQ Test GATE Electrical Engineering (EE) 2023 Mock Test Series | Test: Electrical Machines- 3
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A 6 pole, 12 kW, 240 V DC machine is wave connected. If this machine is now lap connected, all things remaining the same, calculated its power ratings (in kW).
We know that,
P = No. of pole
ϕ = Flux per pale
N = Speed
A = No. of parallel path
A = 2 for wave winding
A = P for lap winding
The emf induced in each coil side of a coil is 10 V and the coil sides lies under opposite poles. The induced emf in them is – (in V)
Since the coil sides lies under opposite poles the induced emf’s in them are additive. Hence it will be 20 V.
How many segments will be there in for the commutator of a 8 pole dc machine having a double layered simple wave wound armature with 86 slots?
For a double layer winding (universally used) number of commutator segments = number of armature coils. The number of slots in double layer winding is equal to the number of coils and the number of commutator segments is also the same.
In an 8 pole dc machine, 60 mechanical degrees correspond to how much electrical degrees?
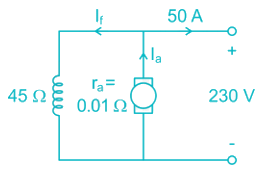
A DC shunt generator delivers 50 A ot terminal voltage of 230 V. The armature and the shunt field resistance are 0.01 Ω and 45 Ω respectively. The stray losses are 400 W. The percentage efficiency of DC generator is _________.
Field current If = 23045 = 5.11A
Armature current Ia = If + IL = 5.11 + 50 = 55.11 A
Stray loss = 400 W
Total loss = 400 + 30.37 + 1175.55 = 1605.92 W
Output power = 230 × 50 = 11500
A 4 pole dc generator has 1200 armature conductors and generates 250 V on open circuit running at a speed of 500 rpm. The diameter of the pole shoe circle is 0.35 m and the ration of pole arc to pole pitch is 0.7 while the length of the shoe is 0.2 m. Find the mean flux density in Tesla in the air gap. Assume lap winding in armature
Pole pitch = distance between two adjacent poles
Area of pole face = pole arc times the axial length
A DC machine is operating as a generator and supplying 8 kW at terminal voltage of 300 V. After a while, it is used as a motor with terminal voltage and armature current remaining same. If the flux per pole is increased by 25% when shifting from generator to motor, what was the change in the speed while doing so, given that the armature resistance is 0.5 Ω ?
When working as generator, armature current, 
= 26.67A
Eg = 300 + (26.67 × 0.5)
= 313.33 V
As motor, Em = V – IaRa
= 300 – (26.67 × 0.5)
= 286.67 V
Now, E α Nϕ
A 6 pole dc generator has 32 slots and 12 conductors per slot. The useful flex per pole is 50 mwb and speed is 1000 rpm. The generator emf is for the lap wound and wave wound respectively
Given that, Number of Poles (P) = 6
Number of slots = 32
Number of conductors = 12 per slot
The conductors (z) = 32 × 12 = 384
Speed (N) = 1000 rpm
Useful flux (∅) = 50 mwb
emf generated
for lap wound machine, A = p
= 320 V
For wave wound machine, A = 2
A separately excited DC generator when running at 1500 rpm, supplies 200 A at 150 V. what will be the load current if speed drops to 1000 rpm. The resistance of armature is 0.25 Ω and voltage drop due to brush contact is 2 V
Load resistance = 150/200 = 0.75Ω
E1 = 150 + (200 × 0.25) + 2
= 202 V
N1 = 1500 rpm, N2 = 1000 rpm
= 134.67 V
V = 134.67 – 0.25 I – 2
I = Load current
V = 132.67 – 0.25 I
A 2-pole DC shunt generator charges a 100 V battery of negligible internal resistance. The armature of the machine is made up of 1000 conductors each of 2 mΩ resistance. The charging currents are found to be 10 A and 20 A for generator speed 1055 and 1105 rpm respectively. Find the field-circuit resistance (in Ω).
Here, the number of pole = 2
As the number of poles are 2, the number of parallel paths for any kind of winding (either lap or wave) = 2
No of conductors connected in a path = 500
Equivalent resistance of a parallel path = 500 × 2 mΩ
Equivalent armature resistance of two parallel paths,
∴ Armature resistance 
At 1055 rpm
Ea1 = Vt + (IL + If) × 0.5 = 100 + (10 + If) 0.5
At 1105 rpm
Ea2 = 100 + (20 + If) × 0.5
Ea1 ∝ N1 ∝ 1055
Ea2 ∝ N2 ∝ 1105
105500 + 10550 + 527.5 If = 110500 + 5525 + 552.5 If
If = 1 A
∴ Field circuit resistance = 
|
22 docs|274 tests
|
|
22 docs|274 tests
|
Download free EduRev App
(Scan QR code)
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
