Test: Electrostatics - 2 - Grade 9 MCQ
15 Questions MCQ Test - Test: Electrostatics - 2
Two spheres of radii r and R carry charges q and Q respectively. When they are connected by a wire, there will be no loss of energy of the system if
In the figure shown, conducting shells A and B have charges Q and 2Q distributed uniformly over A and B. Value of VA − VB is


The electric potential at a point (x,y) is given by: V = −Kxy. The electric field intensity a distance r from the origin varies as
A charge 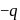 is placed at the axis of a charged ring of radius
is placed at the axis of a charged ring of radius 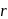 at a distance of
at a distance of 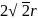 as shown in figure. If ring is fixed and carrying a charge
as shown in figure. If ring is fixed and carrying a charge  , the kinetic energy of charge
, the kinetic energy of charge  when it is released and reaches the centre of ring will be,
when it is released and reaches the centre of ring will be,

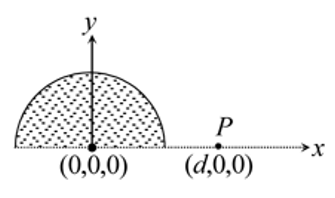
A solid hemispherical uniform charged body having charge Q is kept symmetrically along the y -axis as shown in figure. The electric potential at a distance d from the origin along the x -axis at point P will be
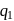 and
and 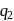 are placed
are placed 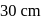 apart as shown. A third charge
apart as shown. A third charge 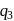 is moved along the arc of a circle of radius
is moved along the arc of a circle of radius 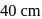 from
from 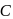 to
to 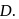 The change in the potential energy of the system is
The change in the potential energy of the system is 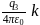 , where
, where 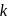 is
is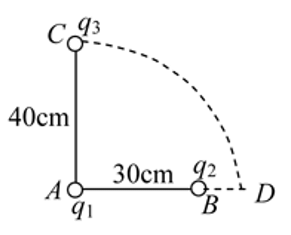
Half part of ring is uniformly positively charged and other half is uniformly negatively charged. Ring is in equilibrium in uniform electric field as shown and free to rotate about an axis passing through its centre and perpendicular to plane. The equilibrium is
A conducting disk is of radius R is rotating with an angular velocity ω allowing the fact that electrons are the current carriers in conductor, the potential difference between the centre of the disc and edge is (mass and charge of electron is m and e and neglect gravity)
Three identical particles, each possessing the mass m and charge +q, are placed at the corners of an equilateral triangle with side r0. The particles are simultaneously set free and start flying apart symmetrically due to Coulomb's repulsion forces. The work performed by Coulomb's forces acting on each particle until the particles fly from one another to a very large distance is (where k = 1/4πε0.)
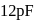 is charged by a battery to a potential difference of
is charged by a battery to a potential difference of 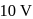 between its plates. The charging battery is now disconnected and a porcelain slab of dielectric constant
between its plates. The charging battery is now disconnected and a porcelain slab of dielectric constant 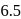 is slipped between the plates. The work done by the capacitor on the slab is
is slipped between the plates. The work done by the capacitor on the slab is
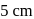 is charged such that the potential on its surface is
is charged such that the potential on its surface is 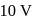 . The potential at a distance of
. The potential at a distance of  from the centre of the sphere is
from the centre of the sphere is
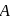 to point
to point 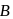 , then
, then
In moving from 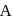 to
to 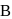 along an electric field line, the work done by the electric field on an electron is
along an electric field line, the work done by the electric field on an electron is 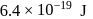 . If
. If 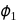 and
and 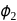 are equipotential surfaces, then the potential difference
are equipotential surfaces, then the potential difference 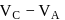 is
is
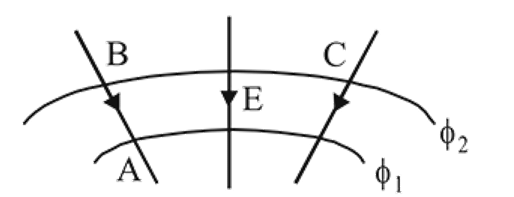
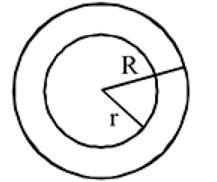
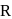 and
and 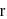 have similar charges with equal surface charge densities
have similar charges with equal surface charge densities 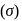 . What is the electric potential at their common centre ?
. What is the electric potential at their common centre ?
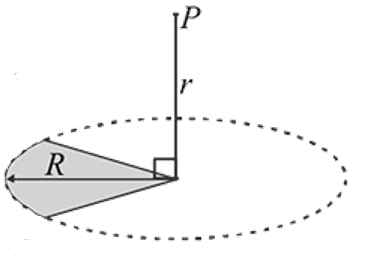
A plastic disc is charged on one side with a uniform surface charge density  and then three quadrant of the disk are removed. The remaining quadrant is shown in figure, with
and then three quadrant of the disk are removed. The remaining quadrant is shown in figure, with 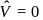 at infinity, the potential due to the remaining quadrant at point
at infinity, the potential due to the remaining quadrant at point  is
is


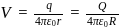 or
or 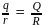
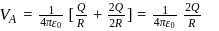
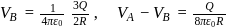

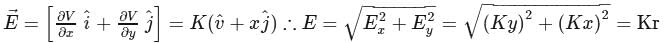
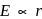
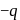 at
at 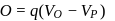
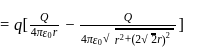
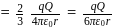
 (c)
(c)
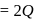
 due to this spherical charge
due to this spherical charge 
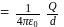
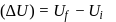
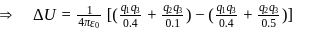

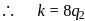
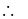 (a)
(a)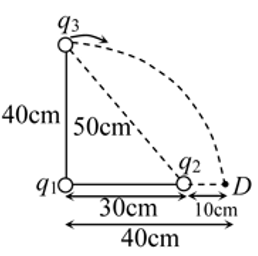
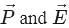 are in same direction, so potential energy
are in same direction, so potential energy 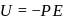
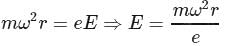
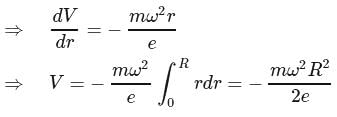
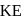 is equal to decrease in P.E.
is equal to decrease in P.E. 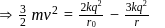
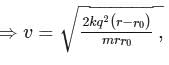
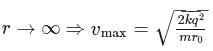
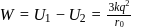

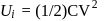
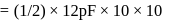
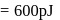
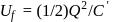
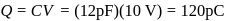
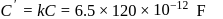
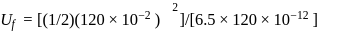
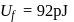
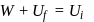
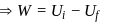
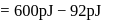
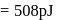
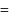 potential at the surface of the sphere
potential at the surface of the sphere 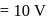 .
.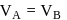
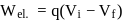
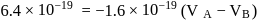
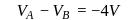
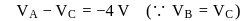
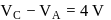
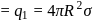 Charge on the inner sphere
Charge on the inner sphere 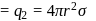
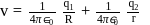
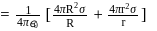
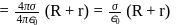
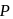 due to whole disc is
due to whole disc is