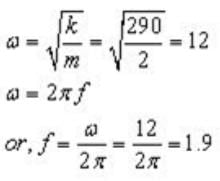Test: Examples of Bodies in Simple Harmonic Motion - Grade 12 MCQ
5 Questions MCQ Test - Test: Examples of Bodies in Simple Harmonic Motion
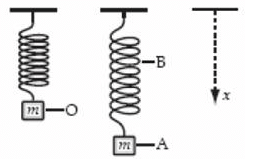
A weight of mass m is at rest at O when suspended from a spring, as shown. When it is pulled down and released, it oscillates between positions A and B. Which statement about the system consisting of the spring and the mass is correct?
What provides the restoring force for SHM in case of column of mercury in U-tube?
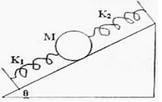
A sphere of mass M is arranged on a smooth inclined plane of angle θ, in between two springs of spring constants K1 and K2 . The springs are joined to rigid supports on the inclined plane and to the sphere (Fig). When the sphere is displaced slightly, it executes simple harmonic motion. What is the period of this motion?

The bob of a pendulum of length, I is pulled aside from its equilibrium position through an angle θ and then released. what will be the speed V of the bob when it pass through its equilibrium condition.
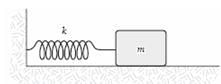
A mass m = 2.0 kg is attached to a spring having a force constant k = 290 N/m as in the figure. The mass is displaced from its equilibrium position and released. Its frequency of oscillation (in Hz) is approximately: