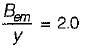Test: Flow Through Open Channels - 1 - Civil Engineering (CE) MCQ
10 Questions MCQ Test GATE Civil Engineering (CE) 2026 Mock Test Series - Test: Flow Through Open Channels - 1
For a wide rectangular channel using Manning’s formula, the differential equation of gradually varied flow (with the usual notations) is given by
The stage in a river is 4.8 m, the water surface- slope is 1 in 10,000 and the discharge in the stream is 600 m3/s. If the stage remains the same and the water surface slope is 1 in 14,400, then the discharge in the stream will be
Water surface profiles that are asymptotic at one end and terminated at the other end would include
For a hydraulically efficient rectangular section, the ratio of width to normal depth is
Consider the following statements in regard to the critical flow:
1. Specific energy is maximum for a given discharge.
2. Specific force is maximum for a given discharge
3. Discharge is maximum for a given specific force.
4. Discharge is maximum for a given specific energy.
Which of these statements are correct?
If F1 and F2 are the Froude numbers of flow before and after the hydraulic jump occurring in a rectangular channel, then
The momentum correction factor for a flow through open channel is given by
The Froude number of a hydraulic jump is 5.5. The jump can be classified as a/an
A hydraulically efficient trapezoidal section of open channel flow carries water at the optimal depth of 0.6 m. Chezy coefficient is 75 and bed slope is 1 in 250. What is the discharge through the channel?
|
31 docs|280 tests
|


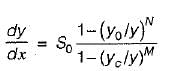

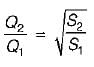
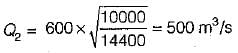

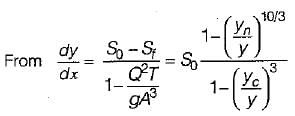
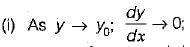 i.e. the water surface approaches normal depth line asymptotically
i.e. the water surface approaches normal depth line asymptotically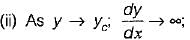 i.e. the water surface meets the criticai depth line vertically in region 2 and 3.
i.e. the water surface meets the criticai depth line vertically in region 2 and 3.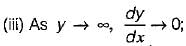 i.e. the water surface meets a very large depth as horizontal asymptote in region 1.
i.e. the water surface meets a very large depth as horizontal asymptote in region 1.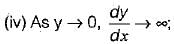 it means that the surface profile meets the channel bed vertically in region 3.
it means that the surface profile meets the channel bed vertically in region 3.