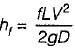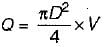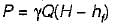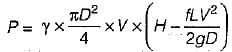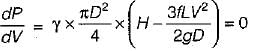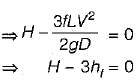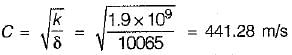Test: Flow Through Pipes - 1 - Civil Engineering (CE) MCQ
10 Questions MCQ Test Topicwise Question Bank for Civil Engineering - Test: Flow Through Pipes - 1
In a pipeline the hydraulic grade line is above the pipe centre line in the longitudinal section at a point A and below the pipe centre line at another point B. From this it can be inferred that
In a horizontal pipe of diameter D and mean velocity of flow V if Δp is the pressure difference between two sections L distance apart, then wall shear stresst ζ0 is given by
Consider the following conditions for the pipe network shown in the given figure (Notations have the usual meaning with suffixes 1, 2 and 3 referring to respective pipes):
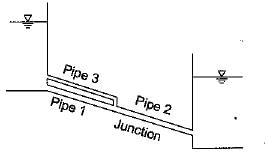
1. Q1 = Q3
2. Q2 = Q1 + Q3
3. hf1 = hf3
4. hf1 = hf2 = hf3
Which of these conditions must be satisfied by this pipe network?

1. Q1 = Q3
2. Q2 = Q1 + Q3
3. hf1 = hf3
4. hf1 = hf2 = hf3
Which of these conditions must be satisfied by this pipe network?
Maximum pressure rise due to water hammer in a pipeline (a = area of the pipe; V0 = Velocity, g = acceleration due to gravity; t = time period; L = length of the pipeline) is
Water of v = 1 centiStoke flows through a 1 cm diameter pipe. Critical flow will correspond to a discharge of approximately
A penstock is 2000 m long and the velocity of pressure wave in it is 1000 m/s. Water hammer pressure head for instantaneous closure of valve at the downstream end of the pipe is 60 m. If the valve is closed in 4 s, then what is the peak water hammer pressure in m of water?
The power transmitted through a pipeline is maximum when the head lost due to friction in the pipe is equal to
Water hammer wave velocity through a rigid pipe conveying sea water with specific weight = 10065 N/m3 and bulk modulus of elasticity = 1.96 x 109 N/m2 is