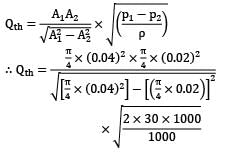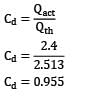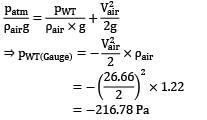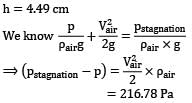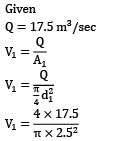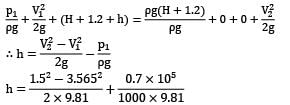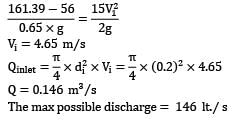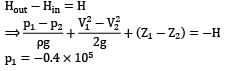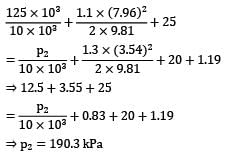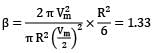Test: Fluid Dynamics Level - 2 - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Fluid Dynamics Level - 2
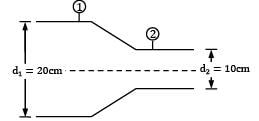
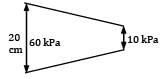
Consider steady, incompressible and irrotational flow through a reducer in a horizontal pipe, where the diameter is reduced from 20 cm to 10 cm. The absolute pressure in the 20 cm pipe just upstream of the reducer is 150 kPa absolute. The fluid has a vapour pressure of 50 kPa absolute and a
specific weight of 5 kN/m3. Neglecting frictional effects, the maximum discharge (in m3⁄sec) that can pass through the reducer without causing cavitation is
A venturi meter of 20 mm throat diameter is used to measure the velocity of water in a horizontal pipe of 40 mm diameter. If the pressure difference between the pipe and throat sections is found to be 30 kPa, and actual discharge is 2.4 Lt/sec. Predict coefficient of discharge for the venturimeter.
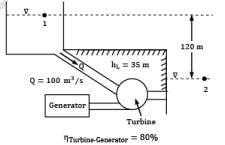
In a hydroelectric power plant, 100 m3 /s of water flows from an elevation of 120 m to a turbine, where electric power is generated (Fig). The total irreversible head loss in the piping system from point 1 to point 2 (excluding the turbine unit) is determined to be 35 m. Estimate the electric power output. (in MW)

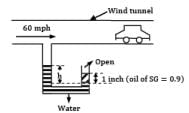
Air is drawn into a wind tunnel used for testing automobiles as shown in Fig. (ρair = 1.22 kg⁄m3 ; 1 mile = 1.6 km 1 inch = 2.54 cm)
(i) Determine the manometer reading h, when the velocity in the test section is 60 mph. Note that there is a 1-in. column of oil on the water in the manometer.
(ii) Determine the difference between the stagnation pressure on the front of the automobile and the pressure in the test section.
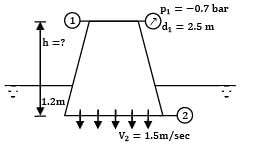
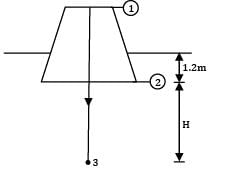
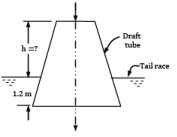
The rate of water through a vertical conical draft tube of a Kaplan turbine is 17.5 m3/s. The diameter of the draft tube on the side connected to the outlet of the turbine runner is 2.5 m and the average velocity at exit is 1.5 m⁄s. If the pressure at inlet to the tube is not to be less than the −0.7 bar, how far the tube should extend above the tail race. Neglect frictional effects and presume that exit of the draft tube lies 1.2 m below the tail water level.
Gasoline flows through a constriction in a horizontal pipe where the diameter is reduced from 20 cm to 10 cm. The pressure in the 20 cm pipe just upstream of constriction is 60 kPa. Considering no loss of energy in the flow passage, make calculations for the maximum discharge (in L/s) that can be passed through the constriction without the occurrence of cavitation. The barometer reads 76 cm of mercury and for gasoline vapour pressure is 56 kPa (abs) and density is 650 kg/m3.
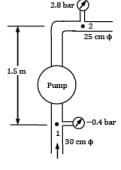
During the test of a centrifugal pump, water was drawn steadily from a reservoir through a vertical 30 cm diameter suction pipe, and the pump discharged the water into a horizontal 25 cm diameter delivery pipe. A Bourdon pressure gauge just outside the casing on the suction pipe read −0.4 bar gauge while the discharge pressure gauge indicated a pressure of 2.8 bar gauge. A vertical distance of 1.5 m intervened between the pipe centers at the sections where the gauges were attached. If the water discharge through the arrangement was measured as 0.1 m3⁄s, compute the power expended in running the pump.
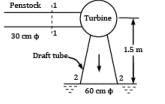
A 30 cm diameter pipe (called penstock) supplies water steadily to a turbine at 0.18 MN/m2. The water leaves the turbine on the exit side through a 60 cm pipe (called draft tube) with a pressure of −0.25 MN/m2. A vertical distance of 1.5 m separates the center of pipes at sections where measurements of pressure have been made. Calculate the power (in kW) delivered to the turbine from water if 0.25 m3 /s of water passes through the arrangement. Neglect frictional losses.
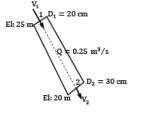
A pipe slopes downwards from 20 cm diameter at upstream section 1 (elevation 25 m) to 30 cm diameter at downstream section 2 (elevation 20 m). A pressure gauge installed at section 1 reads 125 kPa when the water flow rate is 0.25 m3⁄s. If the kinetic energy correction factor for sections 1 and 2 are 1.1 and 1.3 respectively, workout the reading of the pressure gauge at section 2. The loss of head through the pipe may be assumed as 1.2(V1 − V2)2/2g . For the pressure and temperature condition involved, specific weight of water equals 10 kN⁄m3
 .
.
Find the momentum correction factor for the following velocity profile in a circular pipe
![]()
where v is the velocity at any radius r, Vm is the velocity at the pipe axis, and R is the radius of the pipe.