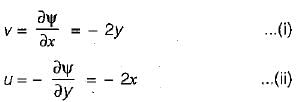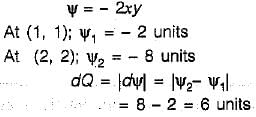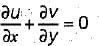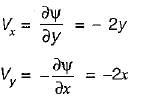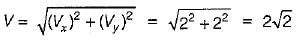Test: Fluid Flow Kinematics - 1 - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Fluid Flow Kinematics - 1
Local acceleration in fluid-flow situations exists only when
A flownet is a graphical representation of streamlines and equipotential lines such that
Stream lines, streak lines and path lines are all identical in case of
Match List-I (Format of representation) with List-ll (Context/Relevant to) and select the correct answer using the codes given below the lists:
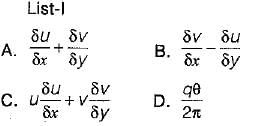
List-ll
1. Relevant to a velocity potential
2. Rate of rotation about a relevant axis
3. Pressure gradient in a relevant direction
4. Continuity of flow

A two-dimensional flow is described by velocity components u = 2x and v = - 2y. The discharge between points (1,1) and (2, 2) is equal to
Consider the following statements in respect of two-dimensional incompressible flow with velocity components u and v in x and y directions respectively:
1. The continuity equation is 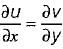
2. The acceleration in x-direction is 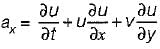
3. The condition of irrotationality is 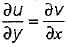
4. The equation of a streamline is udy = -vdx
Which of these statements are correct?
An imaginary tangent at a point which shows the direction of velocity of a liquid particle at that point is
A two dimensional flow field is given by stream function ψ = x2 - y2. The magnitude of absolute velocity at a point (1, 1) is