Test: Functions - Commerce MCQ
15 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Functions
If X = {1, 2, 3, 4}, Y = {1, 2, 3,…., 20}, and f: X → Y be the correspondence which assigns each element in X the value equal to its square, then the domain, co-domain and range of f is
Let X = {1, 2, 3, 4}, Y = {1, 2, …, 10} and f : X –> Y be defined by f(x) = 2x + 1, x ∈ X. Then the range of f is
If f(x) = x2 – x + 1; g(x) = 7x – 3, be two real functions then (f + g)(3) is
The following arrow diagram of the function f : A → A be defined as
If A = {1,2,3}, B = {a,b,c}, which of the following is a function?
The domain and range of the function f: R → R defined by: f = {(x+1, x+5): x ∈ {0, 1, 2, 3, 4, 5}}
Identify the domain and range of the function f(x), defined in N, as below:
If A = {2, 4, 6, 8} and B = {2, 3, 5, 7, 9}. Which of the following is a function from A to B?
|
80 videos|315 docs|99 tests
|



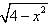 is all real x such that
is all real x such that

















