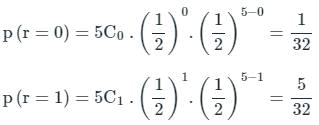Test: Generating Functions - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test - Test: Generating Functions
_____ is a machine that converts mechanical energy into electrical energy.
In an experiment, positive and negative values are equally likely to occur. The probability of obtaining at most one negative value in five trials is
The recurrence T(n) = 2T(n - 1) + n, for n ≥ 2 and T(1) = 1 evaluates to
What is the sequence depicted by the generating series 4 + 15x2 + 10x3 + 25x5 + 16x6+⋯?
What is the generating function for the generating sequence A = 1, 9, 25, 49,…?
What is multiplication of the sequence 1, 2, 3, 4,… by the sequence 1, 3, 5, 7, 11,….?
What is the generating function for the sequence with closed formula an=4(7n)+6(−2)n?
Find the sequence generated by 1/1−x2−x4.,assume that 1, 1, 2, 3, 5, 8,… has generating function 1/1−x−x2.
What is the recurrence relation for the sequence 1, 3, 7, 15, 31, 63,…?
What will be the sequence generated by the generating function 4x/(1-x)2?