Test: Geometry - GMAT MCQ
10 Questions MCQ Test - Test: Geometry
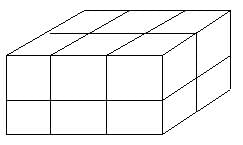
The solid brick shown is made of small bricks of side 1. When the large brick is disassembled into its component small bricks, the total surface area of all the small bricks is how much greater than the surface area of the large brick?
The radius of the front wheels of a cart is half the radius of its rear wheels. If the front wheels have a circumference of 1 meter, and the cart has traveled a distance of 1 kilometer, what is the number of revolutions made by each rear wheel?
The total circumference of two circles is 36. If the first circle has a circumference that is exactly twice the circumference of the second circle, then what is the approximate sum of their two radii?
Mr. Smitherly leaves Cedar Rapids at 8 a.m. and drives north on the highway at an average speed of 50 miles per hour. Mr. Dinkle leaves Cedar Rapids at 8:30 a.m. and drives north on the same highway at an average speed of 60 miles per hour. Mr. Dinkle will
A rectangular tiled patio is composed of 70 square tiles. The rectangular patio will be rearranged so that there will be 2 fewer columns of tiles and 4 more rows of tiles. After the change in layout, the patio will still have 70 tiles, and it will still be rectangular. How many rows are in the tile patio before the change in layout?
The area of a rectangular garden would be increased by 150 square feet if either the length were increased by 7.5 feet or the width were increased by 5 feet. What is the area of the garden, in square feet?
How many vertices does a polygon have, if each vertex is the intersection of exactly three diagonals?
A rectangle with integer side lengths has perimeter 10. What is the greatest number of these rectangles that can be cut from a piece of paper with width 24 and length 60?
Triangle STV has sides ST = TV = 17, and SV = 16. What is the area?




















