Test: Graph Theory - 2 - Electrical Engineering (EE) MCQ
15 Questions MCQ Test - Test: Graph Theory - 2
If [A] Matrix is Incidence matrix then which one of the following is true?
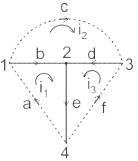
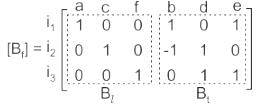
For a network graph having its fundamental loop matrix Bf and its sub-matrices Bt and Bl corresponding to twigs and links, which of the following statements are correct?
1) Bl is always an identity matrix.
2) Bt is an identity matrix.
3) Bf has rank of b – (n – 1), where b is the number of branches and n is the number of nodes of the graph.
Following is not the property of a complete incidence matrix:
Which network topology term got reference directions and marked on the edges of the graph by arrow heads?
If one link fails, the entire network can be disabled in ______.
To construct the dual of a four-mesh network how many nodes are required?
The number of twigs and links in a connected network graph with 'n' nodes and 'b' branches are, respectively.
Considering the principle of duality, which of the following pair is INVALID dual pair?
A loop which does not contain any other loop within it is called _________.
Consider the following data for twigs and links:
N = Number of nodes
L = Total number of links
B = Total number of branches
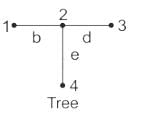
The total number of links associated with a tree is
Consider the following statements regarding trees:
1. A tree contains all the nodes of the graph.
2. A tree shall contain any one of the loops.
3. Every connected graph has at least one tree.
Which of the above statements are correct?
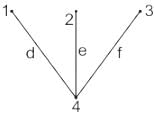
Consider the following with regards to graph as shown in the figure given below:
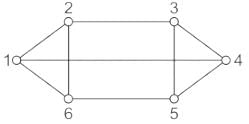
1. Regular graph
2. Connected graph
3. Complete graph
4. Non-regular graph
Which of the above are correct?
What are the properties of a tree in a network graph?
1. It consists of all the nodes of the graph.
2. If the graph has N number of nodes, the tree will have (N – 1) branches.
3. There will be only one closed path in the tree.
If we want to represent a relation between number of link current and number of branch currents in a directional graph, we should use: