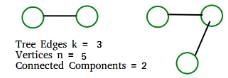Test: Graphs Algorithms- 2 - Computer Science Engineering (CSE) MCQ
25 Questions MCQ Test GATE Computer Science Engineering(CSE) 2026 Mock Test Series - Test: Graphs Algorithms- 2
Consider the following directed graph:

The number of different topological orderings of the vertices of the graph is _____________.
Breadth First Search (BFS) is started on a binary tree beginning from the root vertex. There is a vertex t at a distance four from the root. If t is the n-th vertex in this BFS traversal, then the maximum possible value of n is _________.
Which one of the following algorithm design techniques is used in finding all pairs of shortest distances in a graph?
The most appropriate matching for the following pairs

is:
Consider an undirected unweighted graph G. Let a breadth-first traversal of G be done starting from a node r. Let d(r,u) and d(r,v) be the lengths of the shortest paths from r to u and v respectively in G. if u visited before v during the breadth-first traversal, which of the following statements is correct?
Consider the following graph
Among the following sequences
I. abeghf
II. abfehg
III. abfhge
IV. afghbe
which are depth first traversals of the above graph?
Suppose we run Dijkstra’s single source shortest-path algorithm on the following edge-weighted directed graph with vertex P as the source.
In what order do the nodes get included into the set of vertices for which the shortest path distances are finalized?
Let G1 = (V, E1) and G2 = (V, E2) be connected graphs on the same vertex set V with more than two vertices. If G1 ∩ G2 = (V, E1 ∩ E2 ) is not a connected graph, then the graph G1 ∪ G2 = (V, E1 ∪ E2 )
Consider the undirected graph below:
Using Prim's algorithm to construct a minimum spanning tree starting with node A, which one of the following sequences of edges represents a possible order in which the edges would be added to construct the minimum spanning tree?
Let S and t be two vertices in a undirected graph G=(V,E) having distinct positive edge weights. Let [X,Y] be a partition of V such that s ∈ X and t ∈ Y . Consider the edge having the minimum weight amongst all those edges that have one vertex in X and one vertex in Y
The edge e must definitely belong to:.
In a depth-first traversal of a graph G with n vertices, K edges are marked as tree edges. The number of connected components in G is
In the following table, the left column contains the names of standard graph algorithms and the right column contains the time complexities of the algorithms. Match each algorithm with its time complexity.
To implement Dijkstra’s shortest path algorithm on unweighted graphs so that it runs in linear time, the data structure to be used is:
Let T be a depth first search tree in an undirected graph G. Vertices u and ν are leaves of this tree T. The degrees of both u and ν in G are at least 2. which one of the following statements is true?
Which of the following is the correct decomposition of the directed graph given below into its strongly connected components?
Consider the depth-first-search of an undirected graph with 3 vertices P, Q, and R. Let discovery time d(u) represent the time instant when the vertex u is first visited, and finish time f(u) represent the time instant when the vertex u is last visited. Given that
Which one of the following statements is TRUE about the graph
In an unweighted, undirected connected graph, the shortest path from a node S to every other node is computed most efficiently, in terms of time complexity, by
Consider the DAG with
Which of the following is not a topological ordering?
A depth-first search is performed on a directed acyclic graph. Let d[u] denote the time at which vertex u is visited for the first time and f[u] the time at which the dfs call to the vertex u terminates. Which of the following statements is always true for all edges (u, v) in the graph ?
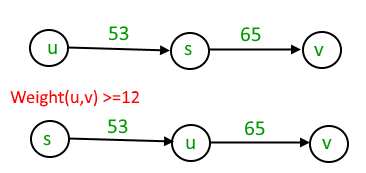
Consider a weighted undirected graph with positive edge weights and let be an edge in the graph. It is known that the shortest path from the source vertex to has weight 53 and the shortest path from to has weight 65. Which one of the following statements is always true?
The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following graph is
Dijkstra's single source shortest path algorithm when run from vertex in the above graph, computes the correct shortest path distance to
The most efficient algorithm for finding the number of connected components in an undirected graph on vertices and edges has time complexity
Consider the following sequence of nodes for the undirected graph given below.
A Depth First Search (DFS) is started at node a. The nodes are listed in the order they are first visited. Which all of the above is (are) possible output(s)?
|
57 docs|215 tests
|
|
57 docs|215 tests
|