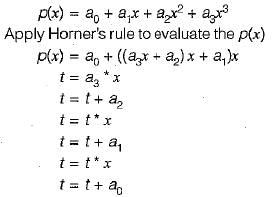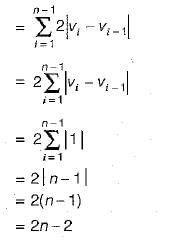Test: Greedy Method - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test Question Bank for GATE Computer Science Engineering - Test: Greedy Method
6 files F1, F2, F3, F4, F5and F6 have 100, 200, 50, 80, 120, 150 records respectively. In what order should they be stored so as to optimize act. Assume each file is accessed with the same frequency.
Which of the following algorithms solves the all pair shortest path problem?
Consider the graph in figure:
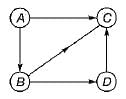
Which of the following is a valid topological sorting?

Kruskal’s algorithm for finding a minimum spanning tree of a weighted graph G with n vertices and m edges has the time complexity of
Let G be an undirected connected graph with distinct edge weights. Let emax be the edge with maximum weight and emin the edge with minimum weight. Which of the following statements is false?
Consider the undirected graph below:
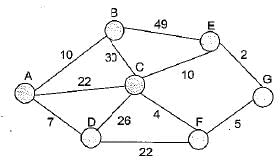
Using Prim’s algorithm to construct a minimum spanning tree starting with node A, which one of the following sequences of edges represents a possible order in which the edges would be added to construct the minimum spanning tree?
In the following table, the left column contains the names of standard graph algorithms and the right column contains the time complexities of the algorithms. Match each algorithm with its time complexity.

Let G{V, E) an undirected graph with positive edge weights. Dijkstra’s single source-shortest path algorithmn can be implemented using the binary heap data structure with time complexity?
Consider the polynominal p(x) = a0 + a1x + a2x2 + a3x3, where 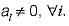 The minimum number of multiplications needed to evaluate p on an input x is
The minimum number of multiplications needed to evaluate p on an input x is
Consider a weighted complete graph G on the vertex set {v1, v2, .... vn} such that the weight of the edge (vi, vj) is 2 | i - j | .The weight of a minimum
|
73 videos|8 docs|165 tests
|
|
73 videos|8 docs|165 tests
|