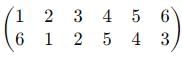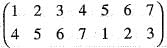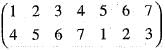Test: Group Theory - 5 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Group Theory - 5
A element aP of a finite cyclic group G of order n is a generator of G iff 0 < p < n and also
Suppose Km = {P∈Sm|, |P| is odd prime}. Determine the set for which m ≥ 3 Km a subgroup of Sm.
If a ∈ G is of order n and P is prime to n, then the order of aP is
A relation (34 × 78) × 57 = 34 × (78 × 57) can have __________ property.
Let R be the ring of all 2 × 2 matrices with integer entries. Which of the following subsets of R is an integral domain?
Statement A : All cyclic groups are abelian.
Statement B: The order of cyclic group is same as the order of its generator.
If f = (2 3) and g = (4 5) be two permutation on five symbols 1, 2, 3,4, 5 then gf is
Statement A : Every isomorphic image of a cyclic group is cyclic.
Statement B : Every homomorphic image of a cyclic group is cyclic
If number of left cosets of H in G are n and the number of right cosets of H in G are m, then
If H1 and H2 are two right coset sets of Subgroup H1, then
|
27 docs|150 tests
|



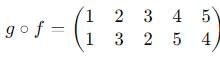
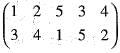 is equal to
is equal to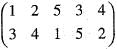 = (135) (24) = (13) (15) (24)
= (135) (24) = (13) (15) (24)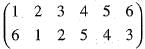 is equivalent to
is equivalent to