Test: Introduction & Properties of Fluid Level- 1 - Mechanical Engineering MCQ
14 Questions MCQ Test Fluid Mechanics for Mechanical Engineering - Test: Introduction & Properties of Fluid Level- 1
A 150 mm diameter shaft rotates at 1500 r. p. m. within a 200 mm long journal bearing with 150.5 mm internal diameter. The uniform annular space between the shaft and the bearing is filled with oil of dynamic viscosity 0.8 poise. The shear stress on the shaft will be
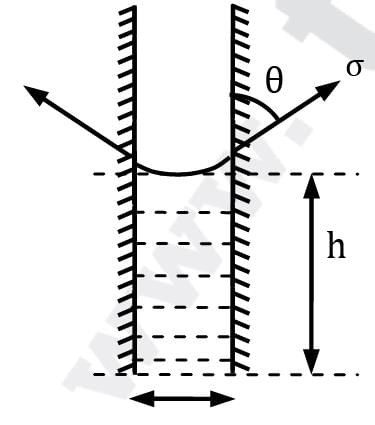
What is the capillary rise in a narrow two dimensional slit of width ‘w’?
In an experiment to determine the rheological behavior of a material, the observed relation between shear stress, τ and rate of shear strain, du / dy is τ = τo + C ( du / dy )0.5
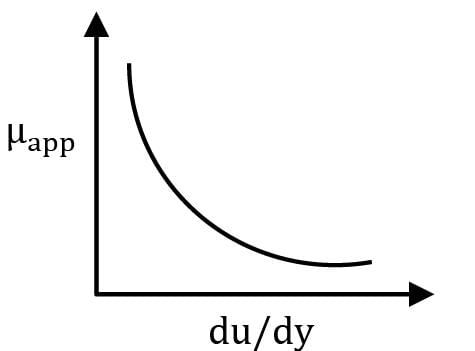
Which of the following represents variation of dynamic viscosity of fluid with rate of shear strain?
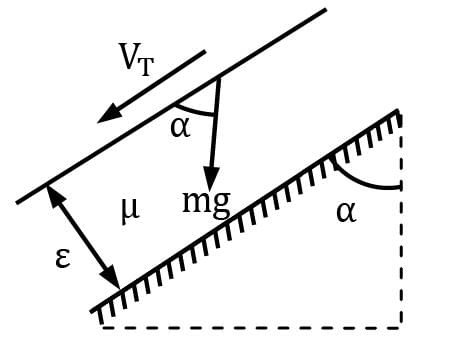
A thin plane lamina of area A and weight W slides down a fixed plane inclined to the vertical at an angle α and maintains a uniform gap ε from the surface of the plane, the gap being filled with oil of viscosity μ. The terminal velocity of the plane is
The figure shows a U-tube having a 5 mm × 5 mm square cross-section filled with mercury (specific gravity=13.6) up to a height of 20 cm in each limb (open to the atmosphere).
If 5cm3 of water is added to the right limb, the new height (in cm, up to two decimal places) of mercury in LEFT limb will be __________
A spherical water drop of 1 mm in diameter splits up in air into 64 smaller drops of equal sizes. The surface tension coefficient of the water air interface is 0.073 N/m. The work required in splitting up the drop is
The velocity distribution over a flat plate is gives by
u = (3 / 4)y − y2
The shear stress at a location 0.3 m above the plate is k times the shear stress at a location 0.2 m above the plate. The value of k is
A beaker is filled with a liquid up to the mark of one litre and weighed. The weight of the liquid is found to be 6.5 N. The specific gravity of the liquid will be
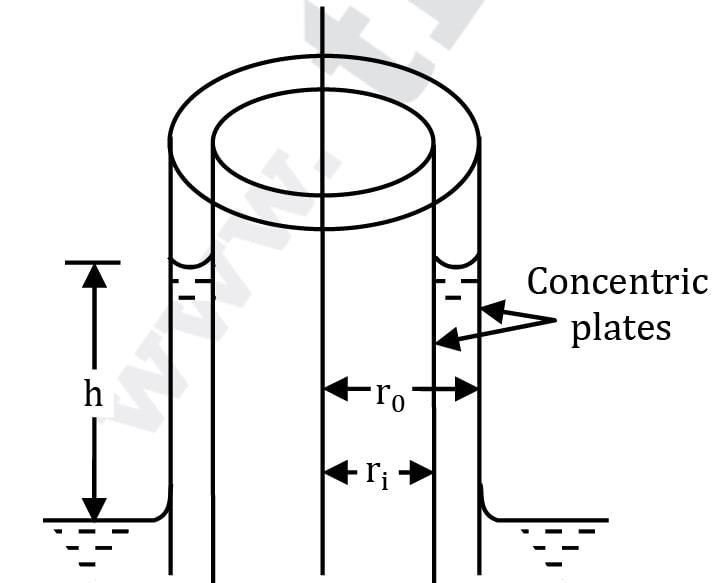
Develop a formula for capillary rise of a fluid having surface tension σ and contact angle θ between two concentric glass tubes of radii r0 and ri
A beaker is filled with a liquid up to the mark of one litre and weighed. The weight of the liquid is found to be 6.5 N. The specific gravity of the liquid will be
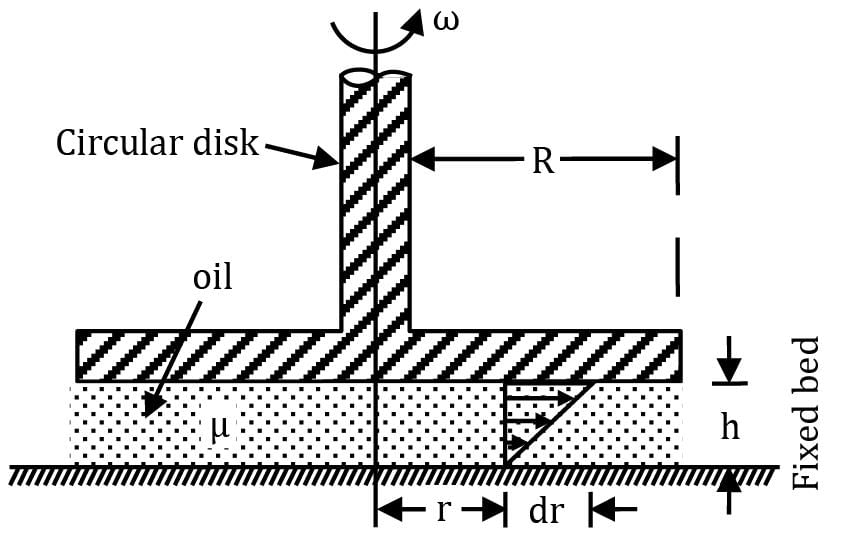
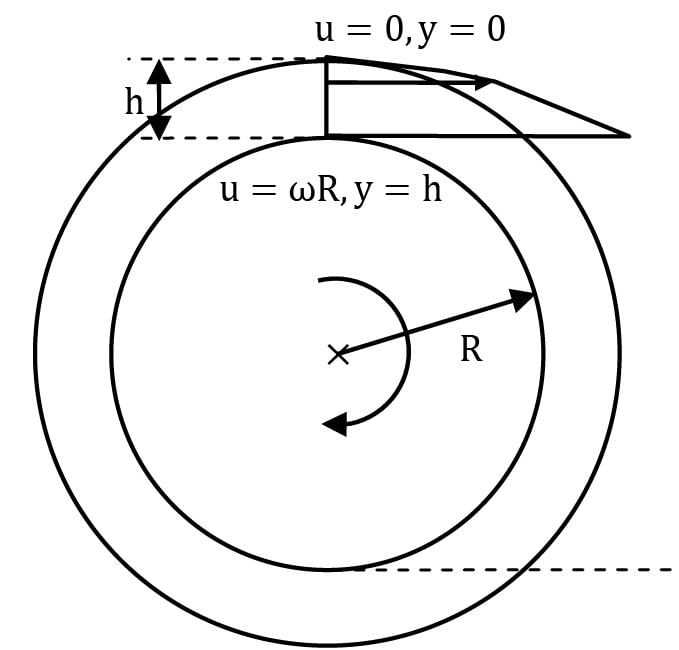
A circular disk of radius R is kept at a small height h above a fixed bed by means of a layer of oil of dynamic viscosity μ. If the disk is rotated at an angular velocity ω, obtain an expression for the viscous torque on the disk. Assume linear variation of velocity within the film.
A pressure vessel initially empty has an internal volume of 0.5 m3 . It is desired to test the vessel at 300 bar by pumping water into it. The estimated increase in volume of containers during the test is 6%. How much water (in kg) is required to be pumped? Consider the bulk modulus of elasticity for water to be 2 GPa.
A hydraulic lift used for lifting automobiles has 20 cm diameter ram which slides in a 20.016 cm diameter cylinder. The annular space between the cylinder and ram is filled with an oil of kinematic viscosity 3.5 strokes and relative density 0.85. If the travel of 3.2 m long ram has a uniform rate of 15 cm/s, estimate the frictional resistance experienced by the ram. answer in kN
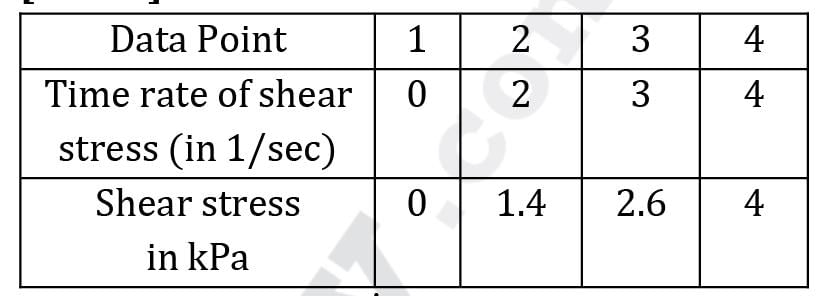
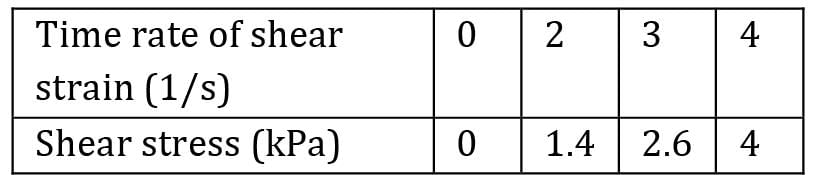
n an experiment, the following shear stress time rate of shear strain values are obtained for a fluid
|
56 videos|106 docs|75 tests
|





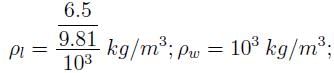 Thus, S = 0:66.
Thus, S = 0:66.