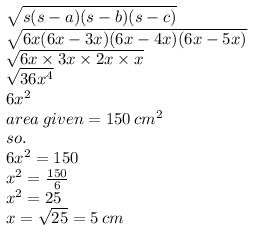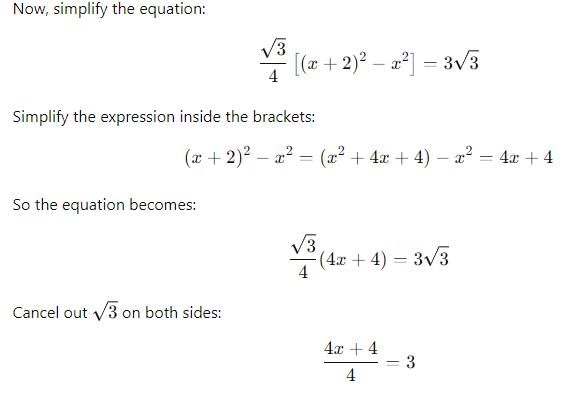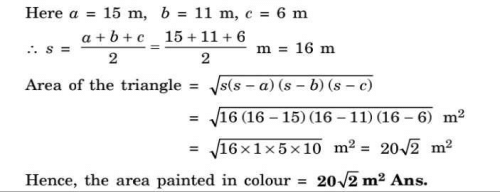Test: Introduction To Heron's Formula
20 Questions MCQ Test Mathematics (Maths) Class 9 | Test: Introduction To Heron's Formula
| 1 Crore+ students have signed up on EduRev. Have you? |
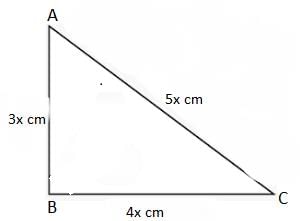
The area of a triangle is 150 cm2 and its sides are in the ratio 3 : 4 : 5. What is its perimeter?
Let coefficient of ratios be X
a = 3x
b = 4x
c = 5x
Using Heron's Formula,
s = (3+4+5)x/2 = 12x/2 = 6x
Now,
a = 5*3 = 15 cm
b = 5*4 = 20 cm
c = 5*5 = 25 cm
Perimeter = 15+20+25 = 60 cm
The area of triangle, whose sides are 15 cm, 25 cm and 14 cm:
Let
a = 15cm
b = 25cm
c = 14cm
Semi-Perimeter = a + b + c / 2
= 15 + 25 + 14 / 2
= 54 / 2
= 27 cm.
Area Through Heron's Formula
= √s(s-a)(s-b)(s-c)
= √27(27-15)(27-25)(27-14)
= √27 × 12 × 2 × 13
= √3 × 3 × 3 × 2 × 2 × 3 × 13
= 3 × 3 × 2 √13
= 18 √13
The area of an equilateral triangle of side 6 cm is
The perimeter of a rhombus is 146 cm. One of its diagonals is 55 cm. The length of the other diagonal and area of the rhombus are
The sides of a triangle are in the ratio of 3 : 4 : 5. If its perimeter is 36 cm, then what is its area?
⇒ AB + BC + CA = 36 cm
⇒ 3x + 4x + 5x = 36 cm
⇒ 12x = 36
⇒ x = 3
∴ AB = 3x = 9
BC = 4x = 12
CA = 5x = 15
Now, (AB)2 + (BC)2
= (9)2 + (12)2
= 81 + 144
= 255
= (AC)2
Δ ABC is a right angle triangle and ∠B is right angle.
Area of Δ ABC = 1/2 (AB x BC)
= 1/2 (9 x12)
= 54 cm2
If each side of an equilateral triangle is increased by 2 cm, then its area increases by 3√3 cm2. The length of its each side and its area are respectively equal to
The area of quadrilateral PQRS, in which PQ = 7 cm, QR = 6 cm, RS = 12 cm, PS = 15 cm and PR = 9 cm:
s = a + b + c /2 = 12 + 9 + 15 /2 = 18cm
Area of PRS = √s(s - a)(s - b)(s - c) = 54 cm^2
s = a + b + c /2 = 7 + 6 + 9 /2 = 11 cm
Area of RPQ = √s(s - a)(s - b)(s - c) = 20.98 cm^2
Area of Quadrilateral = Area of RPQ + Area of PRS
= 54 + 20.98
= 74.98 cm^2
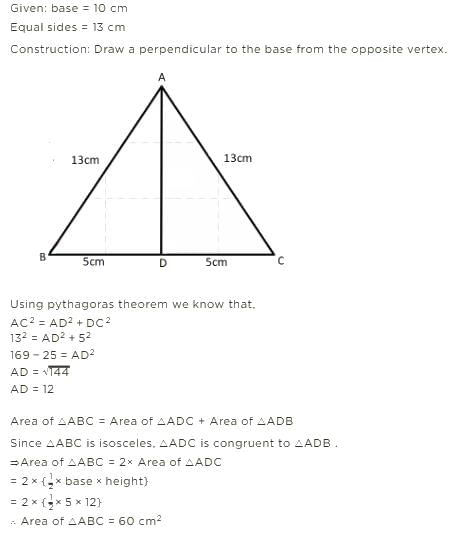
The base of an isosceles triangle is 10 cm and one of its equal sides is 13 cm. The area of the triangle is
The lengths of a triangle are 6 cm, 8 cm and 10 cm. Then the length of perpendicular from the opposite vertex to the side whose length is 8cm is:
The perimeter of an isosceles right angled triangle having an area of 200 cm2 is
Area of isosceles right angled triangle = 1/2 *b*h
Here if it is isosceles right angled triangle ,
Then perpendicular = base = x
So, area =1/2 *x*x
400 = x²
x² = 400
x = = 20 cm
so P = B = 20
By Pythagoras theorem ,
H² = P² +B²
= (20)²+(20)²
= 400 + 400
= 800
H = 20 root 2 cm
Perimeter = 20 + 20 + 20 root 2
= 40+20 root 2
= 68.28 cm
A carpenter had to make a triangle with sides 5, 6, 5 units. By mistake he made one with sides 5, 8, 5 units. The difference between their areas is:
area of actual triangle that he had to make
s = (5+5+6)/2
s= 8
a = √(8 x 3 x 3 x 2)
a1= 12 sq units
area of triangle that the carpenter made
s = (5+5+8)/2
s = 9
a = √(9 x 4 x 4 x 1)
a2 = 12 sq units
so difference a1 - a2 = 12 - 12 =0 sq units
The area of a right triangle of height 15 m and base 20 m is
The sides of a triangle are in the ratio of 3 : 4 : 5. If its perimeter is 36 cm, then what is its area?
The area of an equilateral triangle of side 14 cm is
The sides of a triangle are in the ratio 25 : 17 : 12 and its perimeter is 540m. The area of the triangle is
The perimeter of a triangular field = 540m
Let the sides are 25x , 17x , 12 x
Perimeter of a ∆ = sum of three sides
25x + 17x + 12x = 540
54x = 540
x = 10
1st side (a) - 25x = 25×10= 250m
2nd side(b)= 17x = 17×10= 170m
3rd side (c)= 12x = 12 × 10 =120m
Semi - perimeter ( S) = a+b+c/2
= (250 + 170+120)/2 = 540/2 = 270 m
Area of the ∆= √ S(S - a)(S - b)(S - c)
[By Heron’s Formula]
= √ S(S - 250)(S - 170)(S - 120)
= √ 270(270 - 250)(270 - 170)(270 - 120)
= √ 270× 20×100×150
= √ 81000000
Area of the ∆= 9000 m²
Hence, the Area of the ∆= 9000 m²
The area of an equilateral triangle with perimeter 18x is:
let each side be a
so perimeter is 3a = 18x
a=6x
so area = √3a2/4
=√3*36x2/4
=9x2√3 sq. units
The sides of a triangular plot are in the ratio of 3 : 5 : 7 and its perimeter is 300 m. Its area is
Suppose that the sides, in metres, are 3x, 5x and 7x
Then, we know that 3x + 5x + 7x = 300 (perimeter of the triangle)
Therefore, 15x = 300, which gives x = 20.
So the sides of the triangle are 3 × 20 m, 5 × 20 m and 7 × 20 m
i.e., 60 m, 100 m and 140
= 1500 √(3) = 2598.07621135
The area of a right triangle with base 5 m and altitude 12 m is
There is a slide in a park. One of its side walls has been painted in some colour with a message “Keep the park green and Clean”. If sides of the wall are 15m, 11 m and 6 m, the area painted in colour is________.
The area of a triangle whose sides are 13 cm, 14 cm and 15 cm is
By using herons formula
We get s=13+14+15/2
S=21cm
Now area=√s(s-a) (s-b) (s-c)
√21(21-13)(21-14)(21-15)
√21(8)(7)(6)
√21(336)
√7056
84 cm² is the area.
|
88 videos|397 docs|109 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
88 videos|397 docs|109 tests
|
Download free EduRev App
Related content with Test: Introduction To Heron's Formula
|
|
|
|
Related tests with Test: Introduction To Heron's Formula
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
