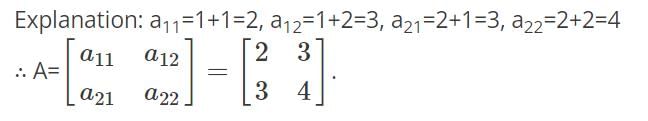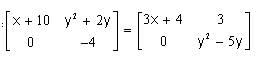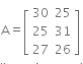Test: Introduction To Matrices
10 Questions MCQ Test Mathematics (Maths) Class 12 | Test: Introduction To Matrices
| 1 Crore+ students have signed up on EduRev. Have you? |
= x+10 = 3x+4
= x = 3
is a matrix of orderSince, there are 2 rows and 2 columns in the matrix, order of the matrix is 2*2.
The number of all the possible matrices of order 2 × 2 with each entry 0 or 1 is
In a 2 × 2 matrix, the total number of elements present are 4. Each element can be replaced with either 1 or 0. Thus, there are two ways of filling each of the four spaces.
Thus the total number of such matrices will be 2×2×2×2 = 2⁴ matrices.
Therefore, the number of possible matrix of 2×2 order with each entry as 0 or 1 is equal to 16.
is example of:A matrix having non-zero elements only in the diagonal running from the upper left to the lower right.
The given matrix is a diagonal matrix.
is a matrix of orderThere are 2 rows and 5 columns in the matrix.
Therefore, order of the matrix: 2 x 5.
What is the element in the 2nd row and 1st column of a 2 x 2 Matrix A = [ aij], such that a = (i + 3) (j – 1)?
Rows are represented by i
Columns are represented by j
... a = (i+3)(j-1)
i = 2 , j = 1 (given)
a21 = (2+3)(1-1) = 0
so, a21 = 0
the value of a22 isaij = 1/2 |i-3j|
As aij = a22 ie i = 2 and j = 2
By substituting the values in the equation, we get
a22 = 1/2 |2-3(2)| = 1/2 |-4| = 2
If the order of the matrix is m×n, then how many elements will there be in the matrix?
The number of elements for a matrix with the order m×n is equal to mn, where m is the number of rows and n is the number of columns in the matrix.
Which of the following is not a possible ordered pair for a matrix with 6 elements?
The possible orders in which the matrix with 6 elements can be formed are 2×3, 3×2, 1×6, 6×1.
Therefore, the possible orders pairs are (2,3), (3,2), (1,6), (6,1). Thus, (3,1) is not possible.
Consider the following information regarding the number of men and women workers in three factories I. II and III
What does the entry in the third row and second column represent if the information is represented as a 3 x 2 matrix?
The information is represented in the form of a 3 X 2 matrix as follows:
The entry in the third row and second column represents the number of women workers in factory III.
|
209 videos|218 docs|139 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
209 videos|218 docs|139 tests
|
Download free EduRev App
Related content with Test: Introduction To Matrices
|
|
|
|
Related tests with Test: Introduction To Matrices
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
