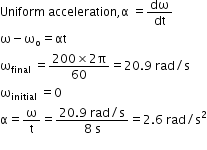Test: Kinematics of Rotational Motion
20 Questions MCQ Test Physics For JEE | Test: Kinematics of Rotational Motion
Direction of linear velocity of a particle rotating in a circular motion is :
Unlike linear motion, where velocity and acceleration are directed along the line of motion, in circular motion the direction of velocity is always tangent to the circle. This means that as the object moves in a circle, the direction of the velocity is always changing. A linear velocity of a particle performing circular motion, which is directed along the tangent to the circular path at given point on the circular path at that instant is called instantaneous velocity. It is also called as tangential velocity.
A ball is under the effect of circular motion about a perpendicular axis with respect to the reference direction. The angular position (in radians) is given by the following function θ = t2 - 0.4t + 2 .The angular position when angular velocity is zero is
Let 
H and 
E respectively be the angular speeds of the hour hand of a watch and that of the earth around its own axis. Compare the angular speeds of the earth and hour hand of a watch.
H and E respectively be the angular speeds of the hour hand of a watch and that of the earth around its own axis. Compare the angular speeds of the earth and hour hand of a watch.Given,
Angular velocity of the hour hand-H
Earth’s speed around its own axis-E
So, time taken by hour hand to complete a rotation is=TH=12hr
Time taken by earth to complete a rotation =TE=24 hours
So,
ωE/ωH =(2π/TE )/2π/TH=TH/TE=1/2
⇒ ωE/ωH=1/2
⇒ 2 ωE= ωH
The angular position of a particle (in radians), along a circle of radius 0.8 m is given by the function in time (seconds) by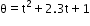 
. The linear velocity of the particle
The answer is option A
So, as we know,
After differentiating angular velocity with respect to t,
Linear velocity=2t+2.3=ω
Now,
Velocity=r x ω(where r is 0.8m)
=0.8x2.3
=1.84m/s
All the points of a rigid body rotating about the given axis have same :
Thus, it is the velocity of a reference point fixed to the body. During purely translational motion (motion with no rotation), all points on a rigid body move with the same velocity. However, when motion involves rotation, the instantaneous velocity of any two points on the body will generally not be the same.
A mixer grinder rotates clockwise, its angular velocity will be :
Clock wise direction means inward field so angular velocity is negative. Anticlockwise means outward field so angular velocity is positive.
Which of the following is not a unit of angular displacement?
Angular displacement is measured in units of radians. 2 pi radians equals 360 degrees. The angular displacement is not a length (i.e. not measured in meters or feet), so an angular displacement is different than a linear displacement.
In an equilateral triangle of length 6 cm , three masses m1= 40g , m2= 60g and m3= 60g are located at the vertices. The moment of inertia of the system about an axis along the altitude of the triangle passing through m1 is
Axis is along AD so Moment of inertia of first mass is zero and 2nd and 3rd masses are at distance of 6/2 from axis, so by using simply I=mr2 we get, I=60×36/4+60×36/4=1080 g cm2
A CD accelerates uniformly from rest to 200 spins per minute in 8 seconds. If the rate of change of speed is constant, determine the instantaneous acceleration in rad/s2 .
A boy is playing with a tire of radius 0.5m. He accelerates it from 5rpm to 25 rpm in 15 seconds. The linear acceleration of tire is
r=0.5m, t=15s
n1=5rpm=5/60 rps
n2=25rpm=25/60rps
… ω1=2π(5) rad/s
… ω2=2π(25) rad/s
As,
a=r∝ [∝=ω2- ω1/t]
so, a=0.5[2π(n2-n1)/t]
a=0.5x6.28x20/60x15
a=6.28x2/60x3
a=6.28/90
a=0.697 m/s2
a≈0.7 m/s2
The angular momentum of a body is 31.4 Js and its rate of revolution is 10 cycle per second. The momentum of inertia of the body about the axis of rotation is
F = w/2π
w = 2πf
w = 2π × 10
w = 62.8
L = Iw
I = L/w
I = 31.4/62.8
I = 0.5 kgm2
Hence A
A merry- go- round ( diameter 4.0 m ) starts from rest and uniformly accelerates until it rotates at 0.8 rev/min. This occurs in 11s. Once it has reached this rate , it rotates at 0.8 rev/min uniformly . Determine the angular acceleration
First we have to find ‘v’ by using the relation v = rw
Now, v = 0.167m/s
Then we find ‘a’ by using the relation a = v/t
So, a = 0.0152m/s2.
Now, we can find angular acceleration by using the formula α = a/r
Finally, α = 0.0076 rad/sec2
A demo CD, 8 cm in diameter, spins 200 rev/min. Determine its linear velocity in cm/s for a point 3 cm from the center.
The Equations of Rotational Motion are
Rotational analogue of force is :
The equation τ = mr2α is the rotational analog of Newton's second law (F=ma), where torque is analogous to force, angular acceleration is analogous to translational acceleration, and mr2 is analogous to mass (or inertia).
A wheel rotates with a constant acceleration of 2.0 rad/s2 . If the wheel starts from rest, the number of revolutions it makes in the first ten seconds will be approximately:
The angular velocity of a second hand of a clock is :
Time taken to complete one rotation is 60 seconds.
One rotation involves 360 degree = 2π
Formula of angular velocity = theta/time taken
Hence, omega = 2π/60
= π/30 rad/s
A car is decelerating uniformly from velocity v1 to velocity v2 while getting displaced by s. If the diameter of the wheel is d, the angular acceleration of the wheel is
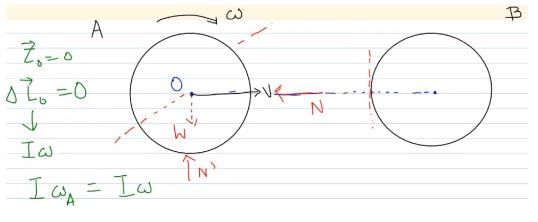
A smooth sphere A is moving on a frictionless horizontal plane with angular speed ω and center of mass velocity v. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωA and ωB respectively. Then
So, “I” gets cancelled.
If n is the frequency of rotation of a body, its angular velocity is:
Related tests
- Test: Kinematics of Rotational Motion
Test | 20 questions | 20 min
- Test: Rotational Motion- 2
Test | 30 questions | 60 min
- Test: Rotational Motion- 1
Test | 30 questions | 60 min
- Rotational Motion Test (27-11-2016)
Test | 30 questions | 60 min
- Rotational Motion MCQ Level - 1
Test | 40 questions | 40 min
|
Follow Us
|