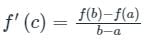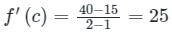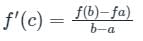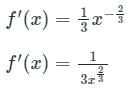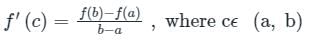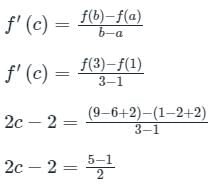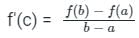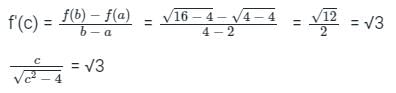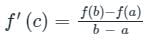Test: Lagrange's Mean Value Theorem - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Lagrange's Mean Value Theorem
A function y = 5x2 + 10x is defined over an open interval x = (1, 2). At least at one point in this interval, dy/dx is exactly
Newton-Gregory Forward interpolation formula can be used ____
A function f(x) = x1/3 -1 ≤ x ≤ 1. The value of 'c' using Lagrange's mean value theorem is ______
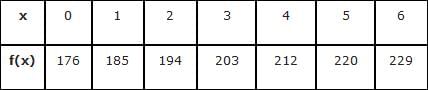
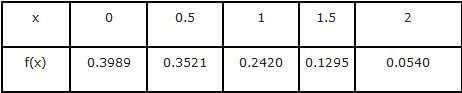
Find n for the following data if f(0.2) is asked.
Let f(x) = x2 - 2x + 2 be a continuous function defined on x ∈ [1, 3]. The point x at which the tangent of f(x) becomes parallel to the straight line joining f(1) and f(3) is
Find n for the following data if f(1.8) is asked.
If the function 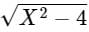 in [2, 4] satisfies the Lagrange’s mean value theorem, then there exists some c ∈ [2, 4]. The value of c is
in [2, 4] satisfies the Lagrange’s mean value theorem, then there exists some c ∈ [2, 4]. The value of c is
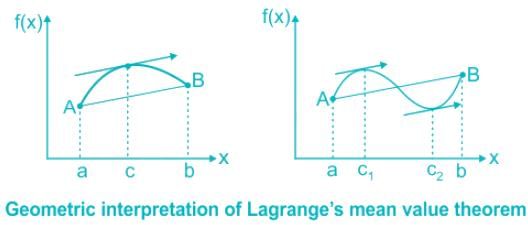
By Lagrange’s mean value theorem which of the following statement is true:
(a) If a curve has a tangent at each of its points then there exists at least one-point C on this curve, the tangent at which is parallel to chord AB
(b) If f’(x) = 0 in the interval then f(x) has same value for every value of x in (a, b)
Find n if x0 = 0.75825, x = 0.759 and h = 0.00005.