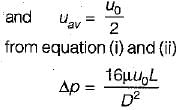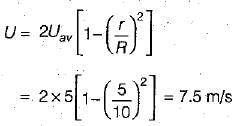Test: Laminar Flow in Pipes - 2 - Civil Engineering (CE) MCQ
6 Questions MCQ Test GATE Civil Engineering (CE) 2026 Mock Test Series - Test: Laminar Flow in Pipes - 2
A fluid of kinematic viscosity 0.4 cm2/sec flows through a 8 cm diameter pipe. The maximum velocity for laminar flow will be
In a two-dimensional flow of a viscous fluid couette flow is defined for
Consider the following statements regarding the laminar flow through a circular pipe:
1. The friction factor is constant.
2. Thp friction factor dspends Upon the pipe roughness.
3. The friction factor varies inversely with the Reynolds number of flow.
4. The velocity distribution is parabolic.
5. The pressure drop varies directly with the mean velocity.
Of these statements:
1. The friction factor is constant.
2. Thp friction factor dspends Upon the pipe roughness.
3. The friction factor varies inversely with the Reynolds number of flow.
4. The velocity distribution is parabolic.
5. The pressure drop varies directly with the mean velocity.
Of these statements:
The velocity profile in fully developed laminar flow in a pipe of diameter D is given by u = u0(1 - 4r2/D2), where r is the radial distance from the center. If the viscosity of the fluid is μ, the pressure drop across a length L of the pipe is
Laminar developed flow at an average velocity of 5 m/s occurs in a pipe of 10 cm radius. The velocity at 5 cm radius is
Consider fully developed laminar flow in a circular pipe of a fixed length:
1) The friction factor is inversely proportional to Reynolds number
2) The pressure drop in the pipe is proportional to the average velocity of the flow in the pipe
3) The friction factor is higher for a rough pipe as compared to a smooth pipe
4) The pressure drop in the pipe is proportional to the square of average of flow in the pipe.
Which of the above statements are correct?
|
31 docs|280 tests
|


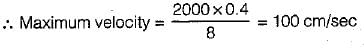

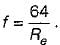 It is neither constant, and does not depend on pipe roughness.
It is neither constant, and does not depend on pipe roughness. 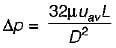 ...(i)
...(i)