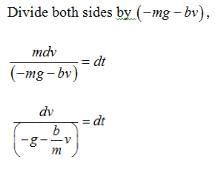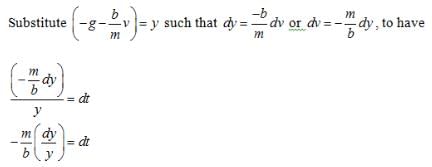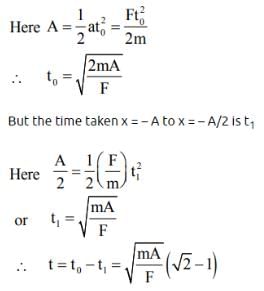Test: Laws of Motion - 2 - JEE MCQ
25 Questions MCQ Test - Test: Laws of Motion - 2
A student calculates the acceleration of m1 in figure shown as a1 = 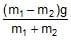 . Which assumption is not required to do this calculation.
. Which assumption is not required to do this calculation.

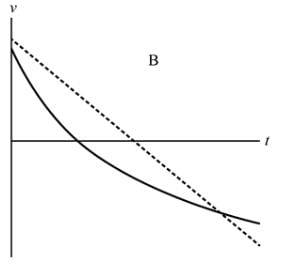
Which graph shows best the velocity-time graph for an object launched vertically into the air when air resistance is given by |D| = bv? The dashed line shows the velocity graph if there were no air resistance.
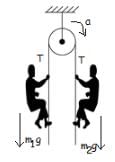
Two men of unequal masses hold on to the two sections of a light rope passing over a smooth light pulley. Which of the following are possible?
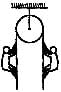
Adjoining figure shows a force of 40 N acting at 30° to the horizontal on a body of mass 5 kg resting on a smooth horizontal surface. Assuming that the acceleration of free-fall is 10 ms_2, which of the following statements A, B, C, D, E is (are) correct?
[1] The horizontal force acting on the body is 20 N
[2] The weight of the 5 kg mass acts vertically downwards
[3] The net vertical force acting on the body is 30 N
For ordinary terrestrial experiments, which of the following observers below are inertial.
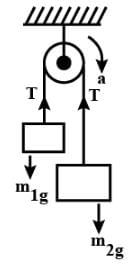
In the system shown in the figure m1 > m2. System is held at rest by thread BC. Just after the thread BC is burnt :
A particle is resting on a smooth horizontal floor. At t = 0, a horizontal force starts acting on it. Magnitude of the force increases with time according to law F = a.t, where a is a constant. For the figure shown which of the following statements is/are correct ?
A cyclist of mass 30 kg exerts a force of 250 N to move his cycle. acceleration is 4 ms−2. force of friction between road and tyres will be
Figure shows the displacement of a particle going along the x-axis as a funtion of time :
A force of magnitude F1 acts on a particle so as to accelerate it from rest to a velocity v. The force F1 is then replaced by another force of magnitude F2 which decelerates it to rest.
A board is balanced on a rough horizontal semicircular log. Equilibrium is obtained with the help of addition of a weight to one of the ends of the board when the board makes an angle q with the horizontal. Coefficient of friction between the log and the board is
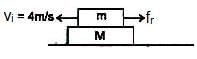
A stationary body of mass m is slowly lowered onto a massive platform of mass M (M >> m) moving at a speed V0 = 4 m/s as shown in fig. How far will the body slide along the platform (μ = 0.2 and g = 10 m/s2)?
A block of mass 2.5 kg is kept on a rough horizontal surface. It is found that the block does not slide if a horizontal force less than 15 N is applied to it. Also it is if found that it takes 5 second to slide throughout the first 10 m if a horizontal force of 15 N is applied and the block is gently pushed to start the motion. Taking g = 10 m/s2, then
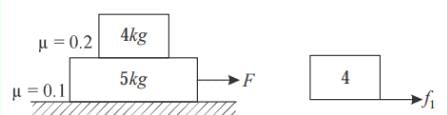
The coefficient of friction between 4 kg and 5 kg blocks is 0.2 and between 5 kg block and ground is 0.1 respectively. Choose the correct statements
In a tug-of-war contest, two men pull on a horizontal rope from opposite sides. The winner will be the man who
A man pulls a block heavier than himself with a light horizontal rope. The coefficient of friction is the same between the man and the ground, and between the block and the ground.
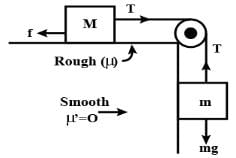
In figure, two blocks M and m are tied together with an inextensible and light string. The mass M is placed on a rough horizontal surface with coefficient of friction m and the mass m is hanging vertically against a smooth vertical wall. The pulley is frictionless.
Choose the correct statement(s)
When a net force act on a body, it produces acceleration in body in direction of net force which is directly proportional to net force acting on body and inversely proportional to its mass. This statement is called
Imagine a situation in which the horizontal surface of block M0 is smooth and its vertical surface is rough with a coefficient of friction m
Identify the correct statement(s)
In above problem, choose the correct value(s) of F which the blocks M and m remain stationary with respect to M0
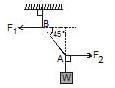
In the figure the tension in the diagonal string is 60 N.
. Find the magnitude of the horizontal force and that must be applied to hold the system in the position shown.
In the above questions what is the weight of the suspended block ?
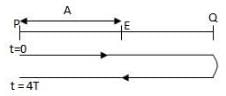
A particle of mass m is constrained to move on x-axis. A force F acts on the particle. F always points toward the position labeled E. For example, when the particle is to the left of E, F points to the right. The magnitude of F is constant except at point E where it is zero.
The system is horizontal. F is the net force acting on the particle. The particle is displaced a distance A towards left from the equilibrium position E and released from rest at t = 0
What is the period of the motion ?