Test Level 1: Binary Logic - CAT MCQ
15 Questions MCQ Test Level-wise Tests for CAT - Test Level 1: Binary Logic
Three persons Bryan, Edward and Avril, each of whom is of a different community, are standing together. When asked about their community, Bryan replied, "I am a Gitty. Avril is Amora.". Then Edward belongs to which community?
Each of three different persons Mary, Helen and Patricia belong to a different community. In the conversation, Patricia said, "I am a Pixie. Mary is not a Gitty.'' Who among the three persons is an Amora?
If Bruce is not a Pixie, then who among the three persons is the Gitty?
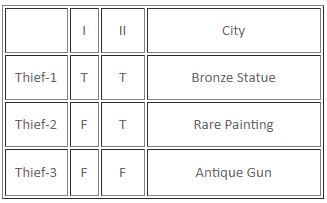
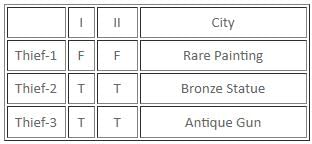
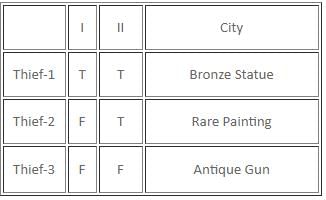
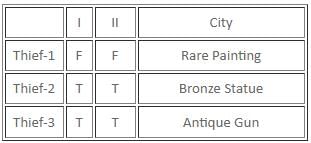
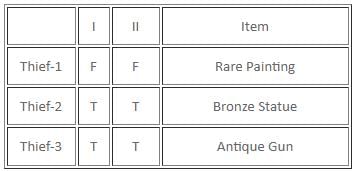
If there are exactly two thieves who always tell the truth and the third thief either always lies or alternates between the truth and a lie, then which of the following statements must be false?
Which of the following statements is/are definitely true?
|
5 docs|272 tests
|