Test Level 1: Speed, Time and Distance - 1 - CAT MCQ
10 Questions MCQ Test Level-wise Tests for CAT - Test Level 1: Speed, Time and Distance - 1
A train takes 8 seconds to pass a pole when it runs at a speed of 36 km/hr. Find the length of the train in metres.
Two trains running at speeds of 36 kmph and 54 kmph, respectively cross each other in 10 sec, if they run in opposite directions. When they run in the same direction, a person sitting in the faster train observes that he crossed the other train in 20 seconds. Find the lengths of the two trains.
The speeds of A and B are in the ratio 2 : 3. Starting from the same position, A takes 10 minutes more than the time taken by B to reach a certain destination. If A had walked at double the speed, then he would have covered the same distance in
Without stoppages, a train travels with an average speed of 40 km/hr, while with stoppages, it covers the same distance with an average speed of 30 km/hr. What is the time (in minutes per hour) for which the train stops?
An express train travelling at a speed of 72 km/hr crosses a goods train travelling at a speed of 45 km/hr in the opposite direction in half a minute. If the express train were to overtake the goods train while moving in the same direction, then how long would it take to do so? (Assume that the trains continue to travel at the same respective speeds as mentioned earlier.)
The Sinhagad Express left Pune at noon sharp. Two hours later, the Deccan Queen started from Pune in the same direction. The Deccan Queen overtook the Sinhagad Express at 8 p.m. Find the average speed of the two trains over this journey if the sum of their average speeds is 70 km/h.
Ram and Bharat travel the same distance at the rate of 6 km per hour and 10 km per hour respectively. If Ram takes 30 minutes longer than Bharat, the distance travelled by each is
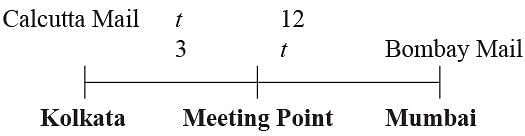
Two trains, Calcutta Mail and Bombay Mail, start at the same time from stations Kolkata and Mumbai respectively towards each other. After passing each other, they take 12 hours and 3 hours to reach Mumbai and Kolkata respectively. If the Calcutta Mail is moving at the speed of 48 km/h, the speed of the Bombay Mail is
Lonavala and Khandala are two stations 600 km apart. A train starts from Lonavala and moves towards Khandala at the rate of 25 km/h. After two hours, another train starts from Khandala at the rate of 35 km/h. How far from Lonavala will they will cross each other?
Alok walks to a viewpoint and returns to the starting point by his car and thus takes a total time of 6 hours 45 minutes. He would have gained 2 hours by driving both ways. How long would it have taken for him to walk both ways?
|
5 docs|272 tests
|



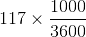 =
= 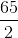 m/sec
m/sec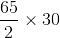 = 975 metres
= 975 metres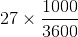 =
= 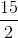 m/sec
m/sec 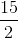 × Time taken (in seconds)
× Time taken (in seconds) 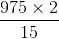 = 130 seconds
= 130 seconds