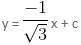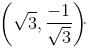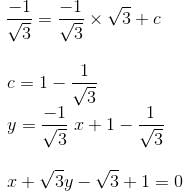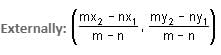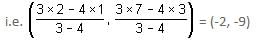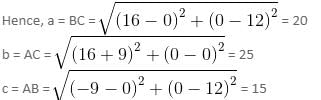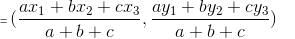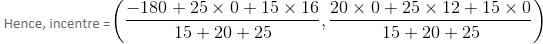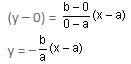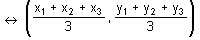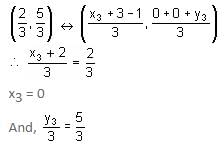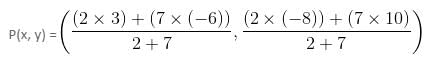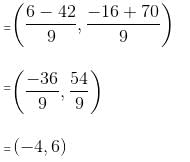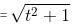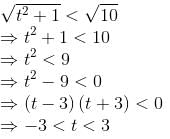Test Level 2: Coordinate Geometry - 2 - CAT MCQ
20 Questions MCQ Test - Test Level 2: Coordinate Geometry - 2
What kind of a quadrilateral is formed by the vertices (0, 0), (4, 3), (3, 5) and (-1, 2)?
If a, b, c are in A.P. then the fixed point through which the straight line ax + 2by + c = 0 will always pass, is
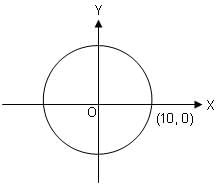
In the above figure, if O(0, 0) is the centre of the circle, then which of the following points lies outside the circle?

Find the equation of a straight line which contains the point 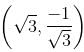 with inclination 150o.
with inclination 150o.
Find the point which divides the line joining the points A (1, 3) and B (2, 7) in the ratio of 3 : 4 externally.
If C is the centroid of the triangle PQR and the coordinates of points P, Q, R and C respectively are (x, 1), (0, y), (1/2, 0) and (1/2, 1/3), find the measure of angle PQR.
In the xy-plane, which of the following points is the greatest distance from the origin?
The projection (the foot of perpendicular) from (x, y) on the x-axis is
If a, b and c are the sides of a triangle, and a2 + b2 + c2 = ab + bc + ca, then the triangle is
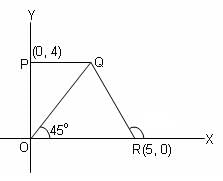
In the given figure, if PQ is parallel to OR, then what is the area of quadrilateral PQRO?
The point that divides the line joining the points (1, 2) and (3, 4) internally in the ratio of 1 : 1 lies in the
The line (1 + K)X + (3 – K)Y = 2(1 + 3K) passes through a fixed point P for any value of K. Find the co-ordinates of P.
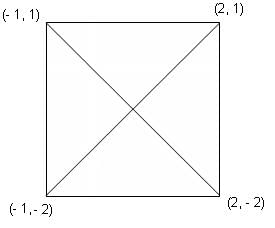
The vertices of a square S have coordinates (-1, -2), (-1, 1), (2, 1) and (2, -2). What are the coordinates of the point where the diagonals of S intersect?
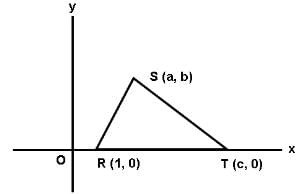
In the rectangular coordinate system shown below, the area of triangle RST is _______.
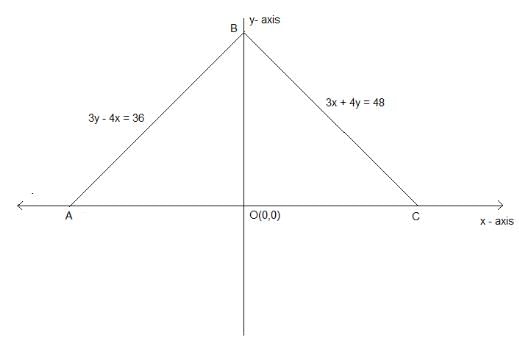
The incentre of a triangle formed by the lines y = 0, 3x + 4y = 48 and 3y - 4x = 36 is
Two points (a, 0) and (0, b) are joined by a straight line. Another point on this line is
If the coordinates of the centroid of a triangle are (2/3, 5/3) and the coordinates of two vertices of the triangle are (-1, 0) and (3, 0), then what are the coordinates of the third vertex of the triangle?
A line segment with end points A(-6, 10) and B(3, -8) is divided in the ratio 2 : 7 by a point P. Find the coordinates of point P.
If point (t, 1) is located inside the circle x2 + y2 = 10, then t must lie between
Find the inclination and perpendicular distance of a line represented by (x/2) + (√3y/2) = 12√5 from the origin.


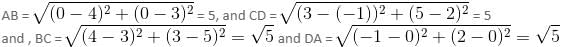
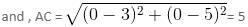

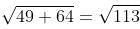 , which is more than 10.
, which is more than 10.