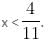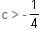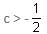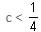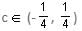Test Level 2: Inequalities - 2 - CAT MCQ
10 Questions MCQ Test Level-wise Tests for CAT - Test Level 2: Inequalities - 2
How many pairs of integers satisfy the inequality |x| + |y| = 7?
It is given that m and n are two real numbers. Which of the following is true for all possible values of m and n?
What is the sum of all possible values of m in the given inequality?
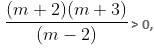 m is an integer, it is known that m ≤ 99.
m is an integer, it is known that m ≤ 99.
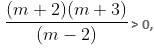 m is an integer, it is known that m ≤ 99.
m is an integer, it is known that m ≤ 99.The number of solutions of the equation 2x + y = 40, where both x and y are positive integers and x ≤ y, is
If 2y - x > 2x - y, and 0 ≤ y ≤ 20, how many non-negative integer pairs of x and y satisfy the given inequalities?
Consider the following system of inequalities:
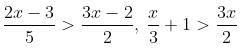
Which of the following options best describes the value of x?
What is the least possible value of c - a if a < b < c and b - a > 5, where a is an even integer and b and c are odd integers?
How many pairs of consecutive odd positive integers, smaller than 18 and having their sum as more than 20, are possible?
If (1 + 3c), 1 and (1 - c) are the three sides of a triangle, then
If x satisfies the inequality |x − 1| + |x − 2| + |x − 3| ≥ 6, then:
|
5 docs|272 tests
|



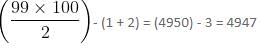

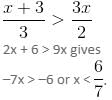
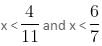 will be satisfied if
will be satisfied if