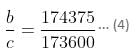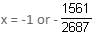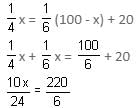Test Level 2: Quadratic Equations & Linear Equations - 1 - CAT MCQ
10 Questions MCQ Test Level-wise Tests for CAT - Test Level 2: Quadratic Equations & Linear Equations - 1
How many positive integer pairs (a, b) satisfy the equation ab = a + b + 20?
In a broken calculator, the keys '+' and '×' have their functions switched. For how many ordered pairs (a, b) of integers will it correctly calculate 'a + b' using the labeled '+' key?
Find the value of x + y, if both x and y are real and x2 + y2 + 2x - 10y = -26.
a, b and c are three numbers, such that ab = 174375 and ac = 173600. b is greater than c by 1. Find the value of b.
The roots of x3 − ax2 + bx − c = 0 are p, q and r, while the roots of x3 + dx2 + ex − 80 = 0 are p + 4, q + 4 and r + 4. What is the value of 16a + 4b + c?
What is the value of 'ab' in the following polynomial identity?
x6 + 1 = (x2 + 1)(x2 + ax + 1)(x2 + bx + 1)
When the sum of two natural numbers is multiplied by each number separately, the products obtained are 2418 and 3666. What is the difference between the two numbers?
The sum of two numbers is 80. If the larger number exceeds four times the smaller number by 5, then find the larger number.
Solve for x: 2687x2 + 4248x + 1561 = 0
One hundred diamonds, each worth Rs. 25,000, are to be divided into two groups, such that one-fourth of the number of diamonds in the first group would be 20 more than one-sixth of the number of diamonds in the second group. What is the ratio of the number of diamonds in the first group to that in the second group?
|
5 docs|250 tests
|


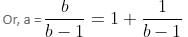
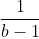 is also an integer. Therefore, b must be 0 or 2, and a also must be 0 or 2, i.e. the ordered pairs are (0, 0) and (2, 2).
is also an integer. Therefore, b must be 0 or 2, and a also must be 0 or 2, i.e. the ordered pairs are (0, 0) and (2, 2).