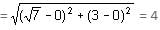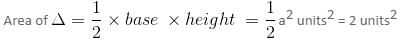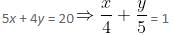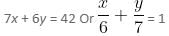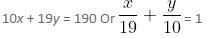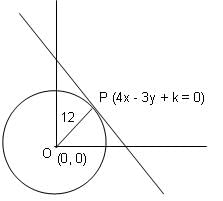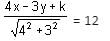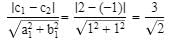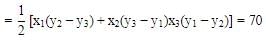Test Level 3: Coordinate Geometry - CAT MCQ
10 Questions MCQ Test - Test Level 3: Coordinate Geometry
Radius of the circle passing through the foci of the ellipse x2/16 + y2/9 = 1 and having its centre at (0, 3) is
If D (2, 1), E (-1, -2) and F (3, 3) are the mid-points of the sides BC, CA and AB, respectively, of the triangle ABC, then the equation of AB is
ABC is an isosceles triangle. If the coordinates of the ends of the base are B (1, 3) and C (-2, 7), then the coordinates of vertex A are
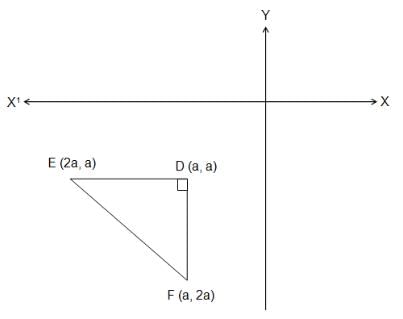
If the points (2a, a), (a, 2a) and (a, a) enclose a triangle of area 2 sq. units, then the value of a is
In which of the following equations are x and y intercepts not consecutive numbers?
If 4x - 3y + k = 0 represents a tangent to the circle x2 + y2 = 144, then what is the value of k?
What is the equation of the line parallel to the line x + 3y = -7 and passing through the centroid of the triangle formed by the intersection of the lines 3x - 4y = -11, 3x - y = -5 and 3x + 2y = 19?
Two sides of a square lie on the lines x + y = 1 and x + y + 2 = 0. What is its area ?
The area of triangle formed by the points (p, 2 − 2p),(1 − p, 2p) and (−4 −p, 6 − 2p) is 70 sq. units. How many integral values of p are possible ?