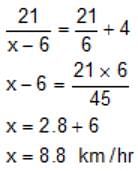Test Level 3: Speed, Time and Distance - CAT MCQ
10 Questions MCQ Test Level-wise Tests for CAT - Test Level 3: Speed, Time and Distance
A train travels at a certain speed for 30 minutes. After that due to a malfunction, it travels at two-thirds of the original speed and reaches its destination 1 hr 30 mins late. Had the malfunction happened after travelling another 60 km, it would have been only 1 hour late. Find the initial speed of the train.
A car travels along a straight line and covers one-third of the total distance at a speed of 4 m/s. Out of the total time taken to cover the remaining distance, it travels at a speed of 2m/s for half the time and at a speed of 6 m/s for the remaining half of time. What is the average speed of the car?
Singapore is 3 hours ahead of Chennai and New Jersey is 11 hours behind India. A flight from Chennai took off at 6 a.m. and reached Singapore at 12 noon and a flight with the same speed takes off from Chennai at 9 a.m. If the distance between Chennai and New Jersey is exactly 4 times the distance between Chennai and Singapore, at what time does the flight, which takes off from Chennai at 9 a.m, reach New Jersey at its local time? (Consider that all the given timings are local timings.)
Saurav and Sachin are running on a 500 m circular track. Their speeds are 8 km/hr and 5 km/hr, respectively. After what time will they meet for the first time at the starting point if they start simultaneously in the same direction?
Two men are walking towards each other alongside a railway line. They both start at opposite ends of a part of the railway track. One man is walking faster than the other. They pass each other 720 yards from the nearer of the two ends. When each man reaches the other end of the track, they stop for a cigarette. Both men take exactly the same amount of time to smoke a cigarette. Then, they turn around and head back to the original starting position. This time they meet 400 yards from the other end of the track. What is the length of the track?
Slow-Run Express runs between Bangalore and Mumbai. For the up as well as the down journey, the train leaves the starting station at 10:00 p.m. everyday and reaches the destination at 11:30 p.m. after three days.
If Mr. Hanni travelled by Slow-Run Express, how many Slow-Run Express trains did Mr. Hanni cross during his journey?
Train A and Train B are running on parallel tracks with the speeds of 72 kmph and 54 kmph, respectively. If they move in the same direction, Mr. Ravi, who sits in the slower train, observes that the faster train passes him in 18 seconds. If they move in opposite directions, both the trains pass each other in 24 seconds. Find the length of the slower train.
Ram and Shyam run around a circular track of length 600 metres. They start simultaneously from the same point and in the same direction. Ram, who runs faster, crosses Shyam in the middle of the 5th round. If Ram and Shyam were to run a 3 km race, how much start in terms of distance should Ram give Shyam so that they finish the race in the same time?
In an event, A rows his boat upstream in a river flowing with a steady speed of 6 km/hr and then returns to the same point without rowing (i.e. only with the speed of river). If the total distance covered by A is 42 km and the time taken in rowing the boat upstream is 4 hours more than his return journey, find the speed of A in still water.
A boat takes 6 hours to travel from A to B (upstream). The river flows at the rate of 2 kmph. How long will the boat take to travel from B to A (downstream), if the distance from A to B is 36 km?
|
5 docs|272 tests
|