Test: Limits And Continuity : Intuitive Approach - 3 - CA Foundation MCQ
30 Questions MCQ Test Quantitative Aptitude for CA Foundation - Test: Limits And Continuity : Intuitive Approach - 3
If f(x) = (x2 -4)÷(x-2) for x<2, f(x)=4 for x=2 and f(x)=2 for x>2, then f(x) at x = 2 is
f(x) = 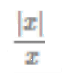 when x o 0, then f(x) is
when x o 0, then f(x) is
If  = i, then which of the following is correct?
= i, then which of the following is correct?
If f(x) = x for 0 ≤ x 1/2, f(x) = 1 for x = 1-x for 1/2<x<1 then at x =1/2 the function is
If f(x)=9x÷(x+2) for x<1, f(1)=3, f(x)=(x+3)x-1 for x>1, then in the interval (-3,3) the function is
Function f(x) = K.x-1 for x < 2
= x-k for x ≥ 2
is continuous at x = 2
The value of 'k' is __________.
The points of discontinuity of the function, F(x) = are
Find limn→∞(2n-1)2n (2n+1)-1 21-n
Find limn→∞[4n2 + 6n +2] ÷ 4n2
Find limn→∞[xn.(n+1)] ÷ [nx n+1 ]
Find limn→∞[n(n+2)] ÷ (n+1)2
Find limn→∞(n3 +a )[(n+1)3a]-1 (2n+1 +a ) (2n +a)-1
Find limn→∞(n2 +1)[(n+1)2 +1]-1 5n+1 5-n
Find limn→∞nn(n+1)-n-1 ÷ n-1
Find limn→∞2n-1 (10 +n) (9+n)-1 2-n
Find limn→∞(1+n-1)[1+2n)-1]-1
Find limn→∞[nn. (n+1)!] ÷ [n! (n+1)n+1]
Find limn→∞[(n+1)n+1. n-n-1 -(n+1).n-1]-n
Find limn→∞[n!3n+1] ÷[3n(n+1)!]
The value of the limit when x tends to zero of the expression (1+n)1/n is
|
114 videos|169 docs|98 tests
|














