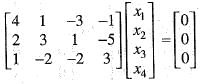Test: Linear Algebra - 1 - Mathematics MCQ
20 Questions MCQ Test - Test: Linear Algebra - 1
If the linear transformation T(v) = Av rotates the vectors (-1, 0) and (0,1), x radians clockwise, then:
If the linear transformation T(v) = Av rotates the vectors v1 = (-1, 0) and v2 = (0, 1) clockwise π radians, the resulting vectors are:
If the linear transformation T(v) = Av rotates the vectors v1 = (-1, 0) and v2 = (0, 1) clockwise π/2 radians, the resulting vectors are:
If the linear transformation T(v) = Av rotates the vectors (-1, 0) and (0, 1) clockwise π/2 radians then:
If A = 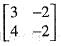 satisfies the matrix equation A2 - kA + 2I = 0, then what is the value of k?
satisfies the matrix equation A2 - kA + 2I = 0, then what is the value of k?
Under which one of the following condition does the system of equations 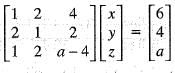 have a unique solution?
have a unique solution?
If the system of equations
x - 2y - 3z = 1, (p + 2)z = 3, (2p + 1)y + z = 2 is inconsistent, then what is the value of P?
If x, y, z are in AP with common difference d and the rank of the matrix  is 2, then the value of d and k are
is 2, then the value of d and k are
The linear transformation T(x, y) = (x + 2y, x - 2y), can be written as a matrix transformation T(x, y) 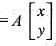 where:
where:
Suppose T1: V ---> U and T2 : U —> W be two linear transformation, Then:
If X = 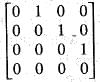 , the rank of XTX, where XT denotes the transpose of X, is
, the rank of XTX, where XT denotes the transpose of X, is
The system of equation kx +y + z = 1,x + ky + z = k and x + y + kz = k3 does not have a solution, if k is equal to


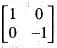 . Then T(v):
. Then T(v):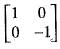
 , then T(v) = Av =
, then T(v) = Av = 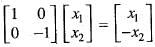
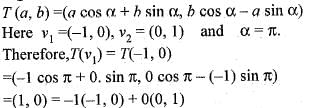
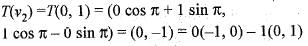
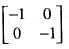

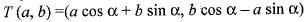 Here v1 = (-1, 0) and a = π
Here v1 = (-1, 0) and a = π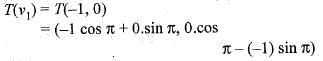
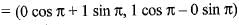
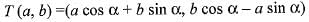
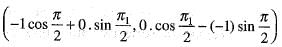 = (0,1)
= (0,1)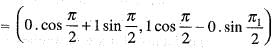
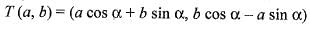
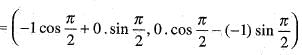
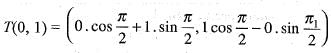
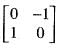
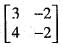 satisfies the equations A2 - kA + 2I = 0.
satisfies the equations A2 - kA + 2I = 0.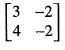
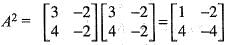
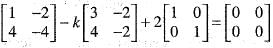 or
or 
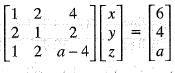



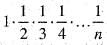
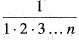
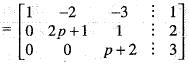
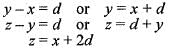
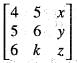 is z.
is z.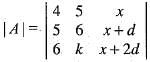
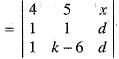
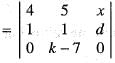
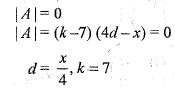
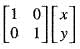 can be written as:
can be written as:
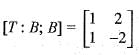
 or equivalently
or equivalently
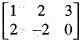 ?
?


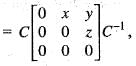 then
then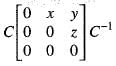 or B is similar to
or B is similar to 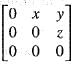 The eigen values of
The eigen values of 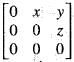 are all zeroes.
are all zeroes. 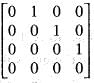
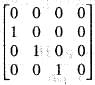

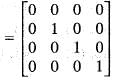
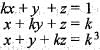
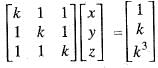
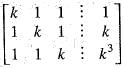
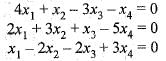 has
has