Test: Linear Algebra - 10 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Linear Algebra - 10
Let {v1, v2, ........,v16} be an ordered basis for V= C16. If T is a linear transformation on V defined by T(v) = vi+1 for 1 ≤ i ≤ 15 and T(v16) = -(v1 + v2 + ... + v16) Then,
Let T : R3 --> R3 be a linear transformation defined by T(x, y, z) =(x + y - z, x + y + z, y - z)
Then, the matrix of the linear transformation T with respect to the ordered basis B = {(0,1,0), (0,0,1), (1,0, 0)| of R3 is
Then, the matrix of the linear transformation T with respect to the ordered basis B = {(0,1,0), (0,0,1), (1,0, 0)| of R3 is
Let T : R4 --> R4 be the linear map satisfying
T{e1) =e2, T(e2) = e3, T(e3) = 0, T(e4) = e3,
where {e1 e2, e3 e4} is the standard basis of R4. Then,
T{e1) =e2, T(e2) = e3, T(e3) = 0, T(e4) = e3,
where {e1 e2, e3 e4} is the standard basis of R4. Then,
Consider the basis {u1 u2, u3} of R3, where u1 = (1, 0, 0), u2 = (1,1,0) , u3 = (1,1,1) . Let {f1, f2, f3} be the dual basis of {u1, u2, u3} and f be a linear functional defined by f(a,b,c) = a + b + c, (a, b, c) ∈ R3. If f = a1f1 + a2f2 + a3f3 then (α1, α2, α3) is
For a matrix [M] = 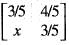 , the transpose of the matrix is equal to the inverse of the matrix [M]' = |M| 1 The value of x is
, the transpose of the matrix is equal to the inverse of the matrix [M]' = |M| 1 The value of x is
If A is a non-zero column vector (n x 1), then the rank of matrix ,AA' is
If P and Q are non-singular matrices, then for matrix M, which of the following is correct?
If the rank of an n x n matrix A is (n - 1), then the system of equations Ax= b has
Let A be a matrix of order m x n and R is non-singular matrix of order n, then
Let A be a square matrix of order n, then nullity of A is
A is a 3 x 4 real matrix and AX = b is an inconsistent system of equations. The highest possible rank of A is
The system of linear equations 4x + 2y =7, 2x + y = 6 has
If x + 2y - 2u = 0, 2x - y - u = 0, x + 2z - u = 0, 4x -y + 3 z - u= 0 is a system of equations, then it is
Let T : P3[0 ,1] --> P2[0 , 1] be defined by (Tp) (x) = P"(x) + P'(x). Then the matrix representation of T with respect to the basis {1, x, x2, x3} and {1, x, x2} of P3[0, 1] and P2[0, 1], respectively is
Let T : R4 —> R4 be defined by
T(x, y , z, w) = (x + y + 5w, x + 2 y + w, - y - z + 2w, 5x + y+ 2z).
Then dimension of the eigen space of T is
|
27 docs|150 tests
|





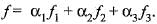
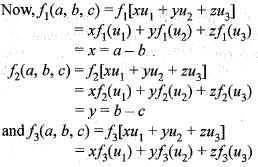
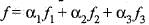
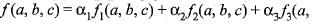
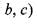
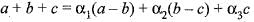 or equivalently
or equivalently 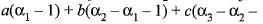
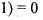
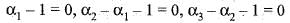
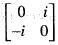 is a
is a then the rank of M is equal to
then the rank of M is equal to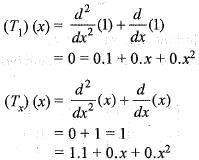
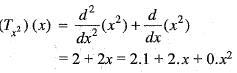 and
and 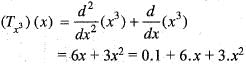

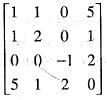 which is a
which is a
















