Test: Linear Algebra - 4 - Mathematics MCQ
20 Questions MCQ Test - Test: Linear Algebra - 4
For a positive integer n, let 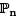 denote the vector space of polynomials in one variable x with real coefficients and with degree < n. Consider the map
denote the vector space of polynomials in one variable x with real coefficients and with degree < n. Consider the map 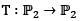 defined by T (p (x)) = p (x2), then
defined by T (p (x)) = p (x2), then
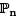 denote the vector space of polynomials in one variable x with real coefficients and with degree < n. Consider the map
denote the vector space of polynomials in one variable x with real coefficients and with degree < n. Consider the map 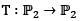 defined by T (p (x)) = p (x2), then
defined by T (p (x)) = p (x2), thenLet A be a real 3 x 4 matrix of rank 2, then the rank of At A, where At deonles the transpose of A. is
Let V be the space of twice differentiable functions 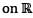 satisfying f" - 2f' + f = 0. Define
satisfying f" - 2f' + f = 0. Define 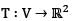 by T(f') = (f'(0), f(0)), then T is
by T(f') = (f'(0), f(0)), then T is
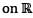 satisfying f" - 2f' + f = 0. Define
satisfying f" - 2f' + f = 0. Define 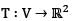 by T(f') = (f'(0), f(0)), then T is
by T(f') = (f'(0), f(0)), then T isWhich of Ihe following matrices has the same row space as the matrix 
The determinant of the n x n permutation 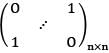
[x] denotes greatest integer function of x.
The row space of a 20 x 50 matrix A has dimention 13. What is the dimension of the space of solution of Ax = 0?
Given a permutation  the matrix A is defined to be the one whose ith column is the σ(i)th column of the Identity matrix I. Which of the following is correct?
the matrix A is defined to be the one whose ith column is the σ(i)th column of the Identity matrix I. Which of the following is correct?
For the matrix A as given below, which of them satisfy A6 = I?
Let I denote the 4 x 4 Identity matrix. If the roots of the characteristic polynomial of a 4 x 4 matrix M 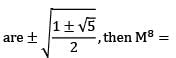
Let M be the set of all invertibel 5 x 5 matrices with entries 0 and 1. For each m ∈ M, let n1 (m) and n0(m) denote the number of 1's and 0's in m respectively then 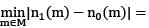
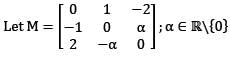 and b a non zero vector such that Mx = b for some
and b a non zero vector such that Mx = b for some  Then the value of xTb is
Then the value of xTb is
Let P be the vector space over 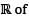 all polynomials of degree less than 3 with real coefficients. Consider the linear transformation T : P → P defined by
all polynomials of degree less than 3 with real coefficients. Consider the linear transformation T : P → P defined by
T(a0 + a1x + a2x2 + a3x3) = a3 + a2x + a1x2 + a0x3
Then the matrix representation of M of T with respect to the ordered basis {1, x, x2,x3} satisfies
Let a,b,c,d be distinct non zero real numbers with a + b = c + d. Then an eigenvalue of the matrix 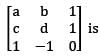
The system of linear equations
x - y + 2z = b1
x + 2y - z = b2
2y - 2z = b3
is inconsistent when (b1, b2, b3) equals
Let X and Y are n x n matrices with real entries, then which of the following is(are) true?



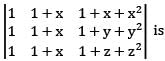
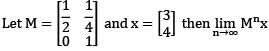
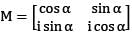 is a unitary matrix when α is
is a unitary matrix when α is