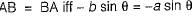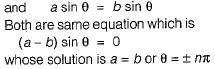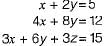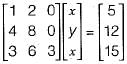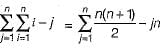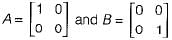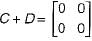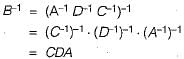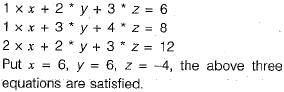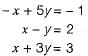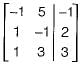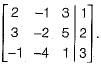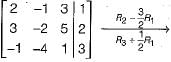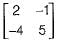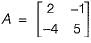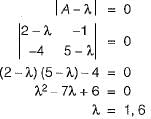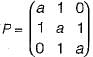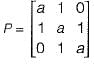Test: Linear Algebra - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test - Test: Linear Algebra
The rank of the following ( n + 1 ) x ( n + 1) matrix, where a is a real number is


Let AX - B be a system of linear equations where A is an m x n matrix and b is a m x 1 column vector and X is an x 1 column vector of unknown. Which of the following is false?
Consider the following set of equations:
x + 2y = 5
4x + 8y = 12
3x + 6y + 3z = 15
This set
An n x n array v is defined as follows:
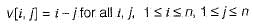
The sum of the elements of the array v is
Consider the following statements:
S1: The sum of two singular n x n matrices may be non-singular
S2: The sum of two n x n non-singular matrices may be singular
Which of the following statements is correct?
Let A, B, C, D be n x n matrices, each with non-zero determinant, If ABCD = I, then B-1 is
What values of x, y and z satisfy the following system of linear equations?
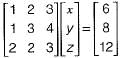
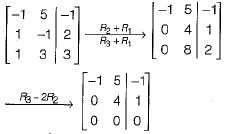
How many solutions does the following system of linear equations have?
- x + 5y = - 1
x - y = 2
x + 3y = 3
Consider the following system of equations in three real variables x1, x2 and x3
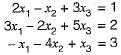
This system of equations has
F is an n x n real matrix, b is an n x 1 real vector. Suppose there are two n x 1 vectors, u and v such that u ≠ v and Fu = b, Fv = b.
Which one of the following statements is false?
If the rank of a (5 x 6) matrix Q is 4, then which one of the following statements is correct?
The trace and determinant of a 2 x 2 matrix are known to be -2 and -35 respectively. It eigenvalues are



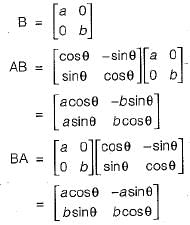
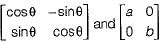 commute under multiplication
commute under multiplication