Test: Matrices & Determinants - 1 - Mathematics MCQ
20 Questions MCQ Test - Test: Matrices & Determinants - 1
If a matrix A is such that 3 A3 + 2 A2 + 5 A + I = 0, then A-1 is equal to
Which of the following statements is/are incorrect?
(i) Adjoint of a symmetric matrix is symmetric.
(ii) Adjoint of a unit matrix is a unit matrix.
(iii) A (adj a) = (adj A) A = |A|
(iv) Adjoint of a diagonal matrix is a diagonal matrix.
(ii) Adjoint of a unit matrix is a unit matrix.
(iii) A (adj a) = (adj A) A = |A|
(iv) Adjoint of a diagonal matrix is a diagonal matrix.
If every minor of order r of a matrix A is zero, then rank of A is
If the eigen values of a square matrix be 1, - 2 and 3, then the eigen values of the matrix 3A are
If the two eigen values of  are 3 and 15, what is the third eigen value?
are 3 and 15, what is the third eigen value?
If A is 3 × 4 matrix and B is a matrix such that A'B and BA' are both defined, then the order of B is
If ω is the cube root of – 1, then the value of 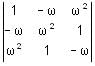 is
is
Let 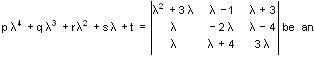 identity inλ, where p, q, r and s are constants, then value of t is
identity inλ, where p, q, r and s are constants, then value of t is
If a = b = c = 0, then the determinant 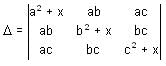 is divisible by
is divisible by
Study the following assertions about a square matrix
(i) The sum of the eigen values of A is equal to its trace
(ii) The product of the eigen values of A is equal to its determinant
(iii) All eigen values of A are non-zero, if and only if A is non-singular
(iv) If A-1 exists, then the eigen-values of A-1 are equal to the reciprocal of the eigen
Q. Which of the following is correct with respect to above assertions?
If ω is an imaginary cube root of unity, then the value of  is
is




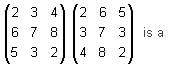
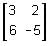 are
are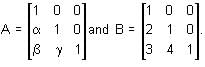 Then
Then is
is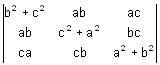 is
is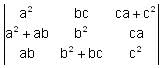 is
is is
is is
is is
is










