Test: Moment Area Theorems - 2 - Civil Engineering (CE) MCQ
12 Questions MCQ Test - Test: Moment Area Theorems - 2
Point A is pin joint and B is roller. A load of 40KN is applied at point C.
Length of AC is 2m and d same goes for beam CB.
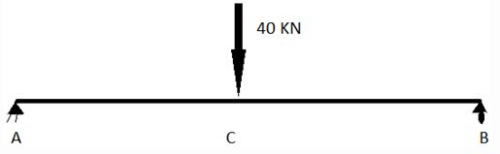
What is the shape for SFD of this diagram?
Length of AC is 2m and d same goes for beam CB.
Point A is pin joint and B is roller. A load of 40KN is applied at point C.
Length of AC is 2m and d same goes for beam CB.
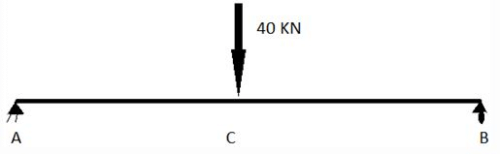
Q. What is the shape of BMD for this diagram?
Length of AC is 2m and d same goes for beam CB.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Point A is pin joint and B is roller. A load of 40KN is applied at point C.
Length of AC is 2m and d same goes for beam CB.
Q. Where is the peak point of SFD?
Length of AC is 2m and d same goes for beam CB.
Point A is pin joint and B is roller. A load of 40KN is applied at point C.
Length of AC is 2m and d same goes for beam CB.
Q. What is the peak value of BMD of this figure (all options are in KN-m)?
Point A is pin joint and B is roller. A load of 40KN is applied at point C.
Length of AC is 2m and d same goes for beam CB.
Q. What should be the area that should be considered if we want to find slope at point B wrt initial beam?
Point A is pin joint and B is roller. A load of 40KN is applied at point C.
Length of AC is 2m and d same goes for beam CB.
Q. What is the value of slope at point B wrt initial beam?
Point A is pin joint and B is roller. A load of 40KN is applied at point C.
Length of AC is 2m and d same goes for beam CB.
Q. To calculate maximum deformation in the deflected beam, which part of the area should be considered?
Point A is pin joint and B is roller. A load of 40KN is applied at point C.
Length of AC is 2m and d same goes for beam CB.
Q. To calculate maximum deformation in deflected beam, about which point should we take moment of the required part of area?
Point A is pin joint and B is roller. A load of 40KN is applied at point C.
Length of AC is 2m and d same goes for beam CB.
Q. What is the value of maximum deformation in this case?
Point A is pin joint and B is roller. A load of 40KN is applied at point C.
Length of AC is 2m and d same goes for beam CB.
Q. To calculate relative deflections of tangents at point A and B at point B, about which point should we moment of the required part of area?
Point A is pin joint and B is roller. A load of 40KN is applied at point C.
Length of AC is 2m and d same goes for beam CB.
Q. To calculate relative deflections of tangents at point A and B at point B, which part of area should be considered?
Point A is pin joint and B is roller. A load of 40KN is applied at point C.
Length of AC is 2m and d same goes for beam CB.
Q. What will be the value of relative deflections of tangents at point A and B at point B?
Top Courses for Civil Engineering (CE)
Important Questions for Moment Area Theorems - 2
Moment Area Theorems - 2 MCQs with Answers
Online Tests for Moment Area Theorems - 2
|
© EduRev
|
Education Revolution
|
Follow Us
|
