Test: Network Topology - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Network Topology
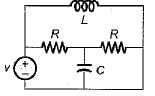
A possible tree of the topology equivalent of the network shown below is

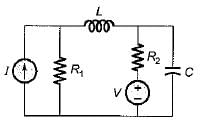
The number of twigs and links in the graph obtained for the given network will be

Consider the following statements concerned with the incidence matrix of a graph:
1. Determinant of the incident matrix of a closed loop is non-zero.
2. Algebraic sum of the row entires of an incidence matrix is zero.
3. If branch j in the graph is not incident at node aij = 0,
Which of the above statements is/are true?
The number of-branches and nodes in the graph are respectively
Assertion (A): When all the elements (i.e. resistors, inductors, capacitors etc.) in a network are replaced by lines with circles or dots at both ends, the configuration is then called the graph of the network.
Reason (R): The graph of any network is drawn by keeping all the points of intersection of two or more branches and representing the network elements of lines, voltages and current sources by their internal impedances.
The graph of a network has N number of nodes and B is the number of branches in it.
Match the List -I and List-II and select the correct answer using the codes given below the lists:


Two graphs are said to be isomorphic graph if their incidence matrices
Assertion (A): The analysis of network is done using Kirchhoffs laws when the values of each element of the network remains constant for all the values of time.
Reason (R): The analysis of a network is done using graph theory when the values of each element of the network are changed with time.