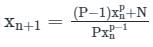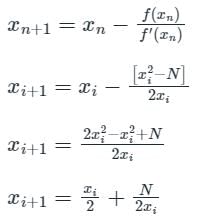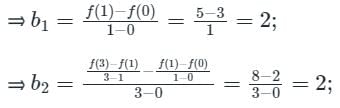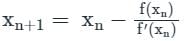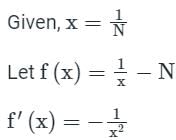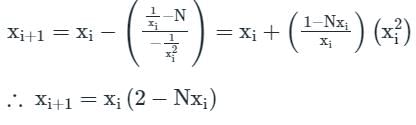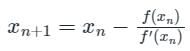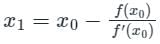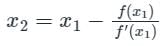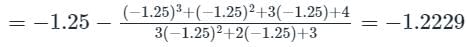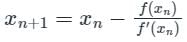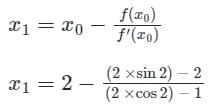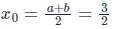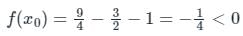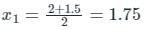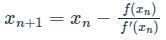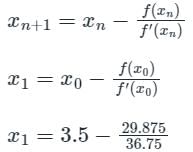Test: Numerical solutions of linear & non-linear algebraic equations - Mechanical Engineering MCQ
10 Questions MCQ Test - Test: Numerical solutions of linear & non-linear algebraic equations
The iteration step in order to solve for the cube roots of a given number Nusing the Newton- Raphson’s method is
The square root of a number N is to be obtained by applying the Newton Raphson iterations to the equation x2 - N = 0, if i denotes the iteration index, the correct iterative scheme will be
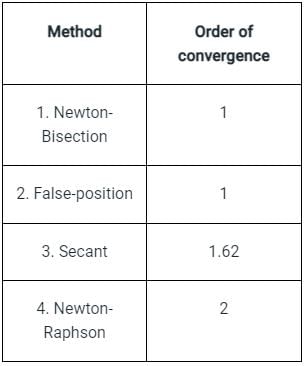
The Newton-Raphson method is said to have
If f(0) = 3, f(1) = 5, f(3) = 21, then the unique polynomial of degree 2 or less using Newton divided difference interpolation will be:
The iteration formula to find the reciprocal of a given number N by Newton’s method is
The real root of x3 + x2 + 3x + 4 = 0 correct to four decimal places, obtained using Newton Raphson method is
To solve the equation 2 sin x = x by Newton-Raphson method, the initial guess was chosen to be x = 2.0. Consider x in radian only. The value of x (in radian) obtained after one iteration will be closest to
The order of convergence of Newton Raphson method is
The 2nd approximation to a root of the equation x2 - x - 1 = 0 in the interval (1, 2) by Bisection method will be:
The approximate value of a root of x3 – 13 = 0, then 3.5 as initial value, after one iteration using Newton-Raphson method, is


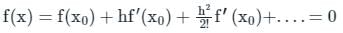
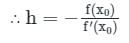
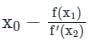 successive approximations are given by x2, x3 ....xn+1 where
successive approximations are given by x2, x3 ....xn+1 where