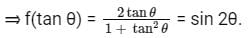Test: Operations on Functions - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test - Test: Operations on Functions
Comprehension:
Read the following information and answer the three items that follow:
Consider the function f(x) = g(x) + h(x)
What is the period of the function g(x) = sin(4x/5) ?
Read the following information and answer the three items that follow:
Consider the function f(x) = g(x) + h(x)
What is the period of the function g(x) = sin(4x/5) ?
If f(x) satisfies the relation 2f(x) + f(1 - x) = x2 for all real x, then f(x) is
Comprehension:
Directions: Read the following information and answer the three items that follow:
Let f(x) = x2 + 2x – 5 and g(x) = 5x + 30
What are the roots of the equation g[f(x)] = 0?
Comprehension:
Read the following information and answer the three items that follow:
Consider the function f(x) = g(x) + h(x)
What is the period of the function 
Comprehension:
Read the following information and answer the three items that follow:
Consider the function f(x) = g(x) + h(x)
What is the period of the function h(x) = cos(2x/3)?
Directions: Read the following information and answer the three items that follow:
Let f(x) = x2 + 2x – 5 and g(x) = 5x + 30
Consider the following statements:
1. f[g(x)] is a polynomial of degree 3.
2. g[g(x)] is a polynomial of degree 2.
Which of the above statements is/are correct?


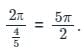

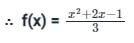

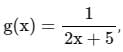 then [(f × g)(5)] =
then [(f × g)(5)] =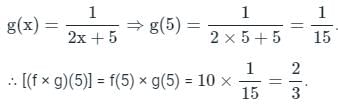
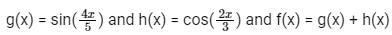
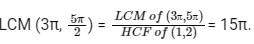
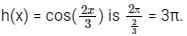


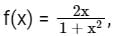 then find the value of f(tan θ).
then find the value of f(tan θ).