Test: Organic Chemistry - JEE MCQ
30 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - Test: Organic Chemistry
In which of the following molecules resonance takes place through out the entire system
In which of the following molecules – NO2 group is not coplanar with phenyl ring ?
In which of the following molecels both phenyl rings are not coplanar ?
In which of the following molecules, all atoms are not coplanar ?
In which of the following, functional group isomerism is not possible?
Rank the following compounds in order of decreasing acidity of the indicated hydrogen :
(i)
(ii)
(iii)
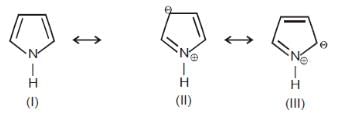
Among these canonical structures, the correct order of stability is
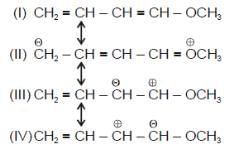
Amongt these canonical structures which one is least stable ?
CH2 = CH – CH = CH – CH3 is more stable than CH3 – CH = C = CH – CH3 because
For phenol which ofthe following resonating structure is the most stable ?
Among these three canonical structures (through more are possible) what would be their relative contribution in the hybrid
The most stable resonating structure of following compound is
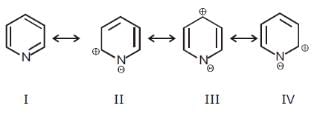
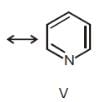
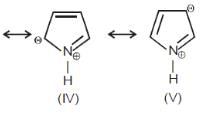
Among these canonical structures of pyridiine, the correct order of stability is
Rank the following compounds in order of decreasing acidity.

Which of the following compounds has maximum electron density in ring ?
In which of the following molecules π-electron density in ring is minimum?
In which of the following molecules π-electron density in ring is maximum?
In which of the following pairs, first species is more stable than second ?
Among these compounds, the correct order of resonance energy is
Rank the following free radicals in order of decreasing stability


Among these compounds, which one has maximum resonance energy ?
There are three canonical structures of napthalene. Examine them and find correct statement among the following:
|
481 docs|964 tests
|