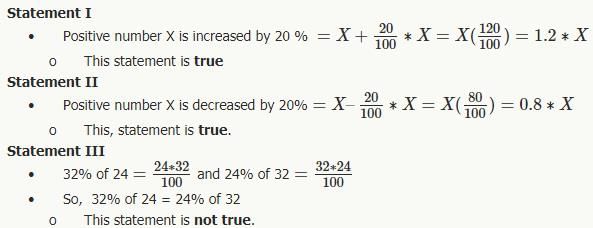Get the App Signup / Login

GMAT Exam > GMAT Tests > Quantitative for GMAT > Test: Percentages- 1 - GMAT MCQ

Test: Percentages- 1 - GMAT MCQ

Test Description

15 Questions MCQ Test Quantitative for GMAT - Test: Percentages- 1

Test: Percentages- 1 for GMAT 2024 is part of Quantitative for GMAT preparation. The Test: Percentages- 1 questions and answers have been prepared according to the GMAT exam syllabus.The Test: Percentages- 1 MCQs are made for GMAT 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Percentages- 1 below.

Solutions of Test: Percentages- 1 questions in English are available as part of our Quantitative for GMAT for GMAT & Test: Percentages- 1 solutions in Hindi for Quantitative for GMAT course. Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free. Attempt Test: Percentages- 1 | 15 questions in 30 minutes | Mock test for GMAT preparation | Free important questions MCQ to study Quantitative for GMAT for GMAT Exam | Download free PDF with solutions

Test: Percentages- 1 - Question 1

Save

What is 1/10 % of 50?

A.
0.005
B.
0.05
C.
0.5
D.
5
E.
500

Detailed Solution for Test: Percentages- 1 - Question 1

⇒ 1/10 % of 50
= 1/10 x 1/100 x 50
= 0.05

Test: Percentages- 1 - Question 2

Save

Find the value of y % of x?

x = 5

x % of y = 2

A.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
B.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
C.
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
D.
EACH statement ALONE is sufficient to answer the question ask
E.
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

Detailed Solution for Test: Percentages- 1 - Question 2

1. we cannot move to any conclusion if we look at the condition number 1 i.e x = 5.
2. Now, x% of y = 2
(x/100)y = 2
xy = 200....Equation 1
Now if we have to calculate y% of x
(y/100)x
yx/100
now putting the value of yx from 1 in equation 2
200/100 = 2
Hence, Statement 2 is sufficient.

1 Crore+ students have signed up on EduRev. Have you? Download the App

Test: Percentages- 1 - Question 3

Save

Which of the following statements are true?

I. If a positive number X is increased by 20% the resulting number would be 1.2X

II.If a positive number X is decreased by 20 % the resulting number would be 0.8X

III.32% of 24 is less than 24% of 32.

A.
I only
B.
II only
C.
III only
D.
I and II only
E.
I, II, and III

Detailed Solution for Test: Percentages- 1 - Question 3

Test: Percentages- 1 - Question 4

Save

A positive number Y is first increased by 10% then decreased by 50% and then increased by 100%. The series of successive changes to Y is equivalent to a single change of

A.
20% decrease
B.
10% decrease
C.
10% increase
D.
20% increase
E.
No change

Detailed Solution for Test: Percentages- 1 - Question 4

Let the number be 100
10% of 100 is 10 = 110 (new Number)
50% of 110 is 55 = 110-55 = 55 (New Number)
100% of 55 is 55= 55+55= 110 (Final Number)
Final Number- Initial Number =110-100=10
And 10 is 10% of 100

Test: Percentages- 1 - Question 5

Save

Restaurant A and Restaurant B decides to roll out a new plan which they believe will get them new customers. Restaurant A decides to give a 10% discount on the original bill amount, and then applies 15% tax on the discounted bill. Restaurant B, on the other hand applies a 15% tax on the original bill amount and then gives a 10% discount on the taxed bill.

If the original bill amount is same for both restaurants, which of the following must be true?

A.
Restaurant A will be 5% cheaper than Restaurant B
B.
Restaurant B will be 5% cheaper than Restaurant A
C.
Restaurant A will be 10% cheaper than Restaurant B
D.
Restaurant B will be 10% cheaper than Restaurant A
E.
Both Restaurants will charge an equal final bill.

Detailed Solution for Test: Percentages- 1 - Question 5

Let the billing amount is 100
Case 1
10% discount on 100 = 10,
So 90 is the taxable amount
15% tax on 90= 13.5.
So total Bill = 90+13.5= 103.5 for Restaurant A
Case 2
15% tax on 100= 115
10 % discount on this is 11.5
Total Bill= 115-11.5= 103.5 for Restaurant B
Hence same in both case

Test: Percentages- 1 - Question 6

Save

If 10 is 5 percent of 10 percent of a number, what is 25% of this number?

A.
5
B.
10
C.
50
D.
500
E.
5000

Detailed Solution for Test: Percentages- 1 - Question 6

Step 1: Let the number be x.
Therefore 10% of x = (10/100)*x = 0.1*x
5% of (10% of x) = (5/100)*0.1*x = 0.05*0.1*x = 0.005*x
Given that this value is equal to 10.
Step 2: Finding required values
Therefore,
0.005*x = 10
⇒ x = (10/0.005) = (10000/5)
⇒ x = 2000
Step 3: Calculating final answer
Therefore, 25% of x = (1/4)*2000 = 500.
Correct Answer: D

Test: Percentages- 1 - Question 7

Save

Karen bought items A, B and C from a supermarket for a total price of $1500. What was the price of item C?

(1) The money she spent to buy item A was 140% of the money she spent to buy the other two items

(2) Item B was 75% less expensive than item C

A.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
B.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
C.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D.
EACH statement ALONE is sufficient.
E.
Statements (1) and (2) TOGETHER are NOT sufficient.

Detailed Solution for Test: Percentages- 1 - Question 7

Steps 1 & 2: Understand Question and Draw Inferences
Let the prices of the items A, B and C be a, b and c dollars respectively.
Given: a + b + c = 1500 . . . Equation 1
We need to find the value of c.
Step 3: Analyze statement 1
As per Statement 1:
The money she spent to buy item A was 140% of the money she spent to buy the other two items
a= 140% of (b+c)
a=140/100(b+c)
a=7/5(b+c)...Equation2
By substituting Equation 2 in Equation 1, we will be able to determine the value of (b + c).
But we will not be able to find the value of c alone.
Therefore, Statement 1 is not sufficient.
Step 4: Analyze statement 2
As per Statement 2:
Item B was 75% less expensive than item C
b = c–75 % of c
b = c−75/100c
b=c/4.........Equation 3
By substituting Equation 3 in Equation 1, we will get an expression in terms of a and c. We will not be determine a unique value for c.
Therefore, Statement 2 is not sufficient.
Step 5: Analyze Both Statements Together (if needed)
From Statement 1:
a = 7(b + c)/5 . . . Equation 2
From Statement 2:
b = c/4 . . . Equation 3
Substituting Equation 2 in Equation 1:
7(b + c)/5 + b + c = 1500
12(b + c)/5 =1500
Solving this equation, we get:
b + c = 625 . . . Equation 4
Substituting Equation 3 in Equation 4:
(c/4 + c) = 625
5c = 625 x 4
c = 500
Thus, we are able to get a unique value of c by using both the statements together.
Therefore, the correct answer is Option C.

Test: Percentages- 1 - Question 8

Save

Tom’s salary has increased by 10% to $11,000. Mike’s salary has reduced by 5%. What is Mike’s current salary if his old salary was two times Tom’s old salary?

A.
$18,000
B.
$19,000
C.
$20,000
D.
$21,000
E.
$22,000

Detailed Solution for Test: Percentages- 1 - Question 8

Step 1: Question statement and Inferences
We are given that the salary of Tom has increased by 10%, and now it has become $11,000, whereas the salary of Mike has decreased by 5%.
It is also given that the old salary of Mike was twice that of Tom's old salary.
Let Tom’s old salary = T_O
Let Mike’s old salary = M_O and Mike’s new salary = M_N
We need to find the value of M_N
Step 2: Finding required values
T_O + 10% of T_O = 11000
⇒ 1.1* T_O = 11000
⇒ T_O = 10000
Therefore Tom’s old salary = $10,000
It is also given that Mike’s old salary is twice Tom’s old salary.
⇒ M_O = 2 * T_O = 20000
Mike’s current salary is 5% less than his old salary.
M_N = M_O – 5% of M_O
⇒ M_N = 0.95*M_O
⇒ M_N = 0.95 * 20000 = 19000
Step 3: Calculating final answer
Therefore Mike’s current salary = $19,000
Correct Answer: B

Test: Percentages- 1 - Question 9

Save

During a housing slump, the number of houses for sale increases by 50% every month. What is the percentage increase in the number of houses on sale after 3 months?

A.
150%
B.
175%
C.
187.5%
D.
212.5%
E.
237.5%

Detailed Solution for Test: Percentages- 1 - Question 9

Step 1: Question statement and Inferences
We are given that during a housing slump, the number of houses for sale increases by 50% every month.
Let the initial number of houses for sale = x
We need to find the number of houses for sale at the end of 3 months to be able to calculate the required percentage increase.
Step 2: Finding required values
Therefore number of houses for sale at the end of the first month = x + 50 % of x =1.5x
Similarly number of houses for sale at the end of the second month = 1.5×(1.5x)=(1.5)²x
Similarly number of houses for sale at the end of the third month = (1.5)³ x = 3.375x
Step 3: Calculating the final answer
Therefore absolute increase in the number of houses = 3.375x−x=2.375x
Therefore the percentage increase in the number of houses compared to the initial number = 2.375x/x×100=237.5%
Correct Answer: E

Test: Percentages- 1 - Question 10

Save

If the tuition fees of University A increased by 25% in four years to $100,000 in the year 2012, by what percent did the tuition fees of University B increase from 2008 to 2012?

(1) In the year 2008, the tuition fees of University A was 2.5 times the tuition fees of University B.

(2) In the year 2012, the tuition fees of University A is $30,000 more than the tuition fees of University B.

A.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
B.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
C.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D.
EACH statement ALONE is sufficient.
E.
Statements (1) and (2) TOGETHER are NOT sufficient.Statements (1) and (2) TOGETHER are NOT sufficient.

Detailed Solution for Test: Percentages- 1 - Question 10

Steps 1 & 2: Understand Question and Draw Inferences
Let tuition fees of University A in 2008 and 2012 be A₀and A₁respectively
Let tuition fees of University B in 2008 and 2012 be B₀and B₁respectively
It is given that:
A₁ = $100,000
And that:
Thus, we have inferred the values of A₀ and A₁ from the question statement.
The question asks us about the percent increase in the tuition fees of University B.
In order to find this percent increase, we need:
(i) Either the values of B₀ and B₁.
(ii) Or, a relationship of the form B₀ = kB₁ where k is a constant
Step 3: Analyze statement 1
As per Statement 1,
In the year 2008, the tuition fees of University A was 2.5 times the tuition fees of University B.
A₀ = 2.5 (B₀)
Since we know the value of A₀, from the above equation, we will be able to find the value of B₀.
However, this statement provides us no clue about the value of B₁ or even about the relationship between B₀ and B₁.
Thus, Statement 1 is not sufficient.
Step 4: Analyze statement 2
As per Statement 2,
In the year 2012, the tuition fees of University A is $30,000 more than the tuition fees of University B
A₁ = B₁ + 30,000
B₁ = 100,000 – 30,000
B₁ = 70,000
However, Statement 2 gives us no idea about the value of B₀ or even about the relationship between B₀ and B₁.
Therefore, Statement 2 is Not Sufficient.
Step 5: Analyze Both Statements Together (if needed)
From Statement 1:
A₀ = 2.5 (B₀)
80000 = 2.5 (B₀)
Thus,
B₀ = 32,000
From Statement 2:
B₁ = 70,000
Thus, we now know the value of B₀ and B₁.
So, we will be able to calculate the percent increase in the tuition fees of University B from 2008 to 2012.
Thus, both the statements together are sufficient to arrive at a unique solution.
Answer: Option (C)

Test: Percentages- 1 - Question 11

Save

In her second attempt of a standardized test, Joan scored 20 percent higher than her first attempt. How much did she score in her second attempt?

(1) Joan scored 200 in her first attempt.
(2) The absolute difference between her two scores was 40 units.

A.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
B.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
C.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D.
EACH statement ALONE is sufficient.
E.
Statements (1) and (2) TOGETHER are NOT sufficient.

Detailed Solution for Test: Percentages- 1 - Question 11

Steps 1 & 2: Understand Question and Draw Inferences
Given that Joan gave two attempts at a standardized test.
Let her score in her first attempt = F.
Given that her score in her second attempt = F + 20% of F = 1.2F
We need to find the value of F to be able to determine her score in the second attempt.
Step 3: Analyze Statement 1
This statement says that Joan scored 200 in her first attempt.
F = 200
Therefore we can calculate her score in her second attempt = 1.2F
Therefore statement 1 is sufficient to arrive at a unique answer.
Step 4: Analyze Statement 2
This statement says that the absolute difference between her scores in the first and second attempts is 40 units.
1.2F – F = 40
0.2F = 40
F = 200.
Since we obtained the value of F, we can calculate the value of 1.2F.
Therefore statement 2 is sufficient to arrive at a unique answer.
Step 5: Analyze Both Statements Together (if needed)
Since we arrived at a unique answer in step 3 and step 4 above, this step is not needed.
Correct Answer: D

Test: Percentages- 1 - Question 12

Save

If Rony’s team played 50% of the total 80 matches conducted in a tournament, what percentage of the matches played by Rony’s team did the team win? (Assume that win and loss are the only possible outcomes. None of the matches ended up in a tie.)

(1) Rony’s team won 60% of the first 30 matches played by them and also won all the remaining matches

(2) The number of matches won by Rony’s team is 133% more than the number of matches lost

A.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
B.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
C.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D.
EACH statement ALONE is sufficient.
E.
Statements (1) and (2) TOGETHER are NOT sufficient.

Detailed Solution for Test: Percentages- 1 - Question 12

Steps 1 & 2: Understand Question and Draw Inferences
Given that total matches played in the tournament = 80.
Number of matches played by Rony’s team (T) = 50% of 80 = 40.
Let the number of matches won by Rony’s team = W.
We need to find the win percentage of Rony’s team = (W/T)*100 = (W/40) * 100
Therefore we need to find the value of W to calculate the win percentage.
Step 3: Analyze Statement 1
The statement says that Rony’s team won 60% of the first 30 matches and then won all of the remaining 10 matches played by them.
So the number of matches won by Rony’s team = W = (60% of 30) + 10 = 18 + 10 = 28.
We know the value of W and therefore we can calculate the required win percentage of Rony’s team.
Therefore Statement 1 is sufficient to arrive at a unique answer.
Step 4: Analyze Statement 2
The statement says that number of matches won by Rony’s team is 133% more than the number of matches lost by them.
Since the total number of matches is 40, the number of matches lost = (40 – W).
Therefore
W = (40 – W) + 133% of (40 –W)
W = (40 – W) + (4/3)*(40 – W)
(Note that since 33% is equivalent to 1/3, 133% is equivalent to 4/3)
3W = 280 – 7W
W = 28
Therefore statement 2 is sufficient to arrive at a unique answer.
Step 5: Analyze Both Statements Together (if needed)
We arrived at a unique answer in step 3 and step 4 above. So this step is not needed.
Correct Answer: D

Test: Percentages- 1 - Question 13

Save

Jack made a withdrawal from his savings account to fund a medical emergency. What was the percent decrease in his savings fund, if his savings fund post withdrawal will need to be increased by 25 percent to be restored to its initial amount?

A.
10%
B.
20%
C.
25%
D.
40%
E.
50%

Detailed Solution for Test: Percentages- 1 - Question 13

Step 1: Question statement and Inferences
Let the withdrawal from the fund be p%
Let the initial amount be X
Balance after withdrawal = B = X -p% of X
Step 2: Finding required values
We are also given that B needs to be increased by 25% to bring it back to X.
Step 3: Calculating the final answer
Substitute Equation (1) in Equation (2):
5(100−p)=400
500–5p=400
5p=100
p=20%
Thus, the withdrawal from the fund was 20%
Answer: Option (B)

Test: Percentages- 1 - Question 14

Save

The number of students in a class is 25, of which 40% are girls. How many more girls must be added in the class such that the percentage of girls is double the current percentage?

A.
5
B.
10
C.
15
D.
20
E.
50

Detailed Solution for Test: Percentages- 1 - Question 14

Step 1: Question statement and Inferences
The important thing to keep in mind in this question is that when more girls are added to the class, the total number of students will also increase.
Step 2: Finding required values
Originally:
Number of girls = G = 40% of 25
G = 40/100 × 25
G = 10
After adding more girls:
Let x number of girls be added
So, number of girls now =G' = 10 + x
Total number of students now = 25 + x
Step 3: Calculating the final answer
It’s given that:
Thus, the number of girls added = 50
Looking at the answer choices, we see that Option E is correct

Test: Percentages- 1 - Question 15

Save

Last year country X won 15 gold medals in total 60 competitions. This year country X won only 5 gold medals in a total of 50 competitions. What is the percentage reduction in the percentage of gold medals won per competition this year vs last year?

A.
15%
B.
40%
C.
60%
D.
80%
E.
100%

Detailed Solution for Test: Percentages- 1 - Question 15

Step 1: Question statement and Inferences
We are given that last year country X won 15 gold medals in a total of 60 competitions. However, this year country X won only 5 gold medals in a total of 50 competitions.
We have to find the percentage reduction in the percentage of gold medals won per competition.
Step 2: Finding required values
Now, to calculate the required percentage reduction, we need to first calculate the percentage of gold medals won by country X this year and the similar percentage for last year.
Percentage of gold medals (to competitions) this year = (5/50)*100 = 10%
Percentage of gold medals (to competitions) last year = (15/60)*100 = 25%
Step 3: Calculating final answer
We are talking about the reduction in percentage compared to last year.
Therefore the required percentage = [(25 – 10)/25]*100 = 15*4 = 60%
Correct Answer: C

	Quantitative for GMAT 115 videos\|106 docs\|113 tests

Quantitative for GMAT

115 videos|106 docs|113 tests

Join Course

Information about Test: Percentages- 1 Page

In this test you can find the Exam questions for Test: Percentages- 1 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Percentages- 1, EduRev gives you an ample number of Online tests for practice

Top Courses for GMAT

	Quantitative for GMAT 115 videos\|106 docs\|113 tests

Quantitative for GMAT

115 videos|106 docs|113 tests

Join Course

Download as PDF

Top Courses for GMAT

Join with a free account

Get Instant Access to 1000+ FREE Docs, Videos & Tests

10,000,000

Users

100+

Exams

3,25,000

Docs and Videos

75,000

Tests

I have an EduRev Account • Sign Up with Email

Attempt this test on App!

Get detailed analysis along with solutions of each question.

Open in App

Not Now

Schools

Medical
Non- Medical
Commerce
Humanities
CBSE Class 10
CBSE Class 9
CBSE Class 8
CBSE Class 7
CBSE Class 6
CBSE Class 5
CBSE Class 4
CBSE Class 3
CBSE Class 2
CBSE Class 1

Competitive Examinations

UPSC
NEET
JEE
CLAT
CAT
GMAT
GATE
Railways
SSC
IIT JAM
Defence
Insurance
Teaching
CA Foundation

Technical Exams

GATE
SSC JE
RRB JE
Civil Engineering
Computer Science Engineering
Electrical Engineering
Electronics Engineering
Biotechnology Engineering
Mechanical Engineering
Chemical Engineering

Important Questions for Percentages- 1

Find all the important questions for Percentages- 1 at EduRev.Get fully prepared for Percentages- 1 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Percentages- 1 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Percentages- 1 resources.

Percentages- 1 MCQs with Answers

Prepare for the Percentages- 1 within the GMAT exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Percentages- 1 Quantitative for GMAT

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Percentages- 1 with ease. Join thousands of successful students who have benefited from our trusted online resources.

Education Revolution