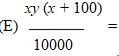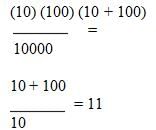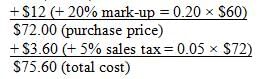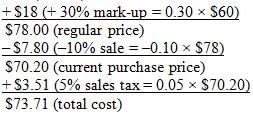Test: Percentages- 3 - UPSC MCQ
15 Questions MCQ Test - Test: Percentages- 3
Two years ago, Arthur gave each of his five children 20 percent of his fortune to invest in any way they saw
fit. In the first year, three of the children, Alice, Bob, and Carol, each earned a profit of 50 percent on their
investments, while two of the children, Dave and Errol, lost 40 percent on their investments. In the second
year, Alice and Bob each earned a 10 percent profit, Carol lost 60 percent, Dave earned 25 percent in profit,
and Errol lost all the money he had remaining. What percentage of Arthur's fortune currently remains?
fit. In the first year, three of the children, Alice, Bob, and Carol, each earned a profit of 50 percent on their
investments, while two of the children, Dave and Errol, lost 40 percent on their investments. In the second
year, Alice and Bob each earned a 10 percent profit, Carol lost 60 percent, Dave earned 25 percent in profit,
and Errol lost all the money he had remaining. What percentage of Arthur's fortune currently remains?
A car dealership has 40 cars on the lot, 30% of which are silver. If the dealership receives a new shipment of
80 cars, 40% of which are not silver, what percent of the total number of cars are silver?
80 cars, 40% of which are not silver, what percent of the total number of cars are silver?
Paul's income is 40% less than Rex's income, Quentin's income is 20% less than Paul's income, and Sam's
income is 40% less than Paul's income. If Rex gave 60% of his income to Sam and 40% of his income to
Quentin, Quentin's new income would be what fraction of Sam's new income?
income is 40% less than Paul's income. If Rex gave 60% of his income to Sam and 40% of his income to
Quentin, Quentin's new income would be what fraction of Sam's new income?
A school’s annual budget for the purchase of student computers increased by 60% this year over last year. If
the price of student computers increased by 20% this year, then the number of computers it can purchase
this year is what percent greater than the number of computers it purchased last year?
Boomtown urban planners expect the city’s population to increase by 10% per year over the next two years.
If that projection were to come true, the population two years from now would be exactly double the
population of one year ago. Which of the following is closest to the percent population increase in Boomtown
over the last year?
A retailer bought a shirt at wholesale and marked it up 80% to its initial retail price of $45. By how many
more dollars does he need to increase the price to achieve a 100% markup?
A certain NYC taxi driver has decided to start charging a rate of r cents per person per mile. How much, in
dollars, would it cost 3 people to travel x miles if he decides to give them a 50% discount?
Bob just filled his car's gas tank with 20 gallons of gasohol, a mixture consisting of 5% ethanol and 95%
gasoline. If his car runs best on a mixture consisting of 10% ethanol and 90% gasoline, how many gallons of
ethanol must he add into the gas tank for his car to achieve optimum performance?
A certain tank is filled to one quarter of its capacity with a mixture consisting of water and sodium chloride.
The proportion of sodium chloride in the tank is 40% by volume and the capacity of the tank is 24 gallons. If
the water evaporates from the tank at the rate of 0.5 gallons per hour, and the amount of sodium chloride
stays the same, what will be the concentration of water in the mixture in 2 hours?
The useful life of a certain piece of equipment is determined by the following formula: u =(8d)/h2, where u is
the useful life of the equipment, in years, d is the density of the underlying material, in g/cm3, and h is the
number of hours of daily usage of the equipment. If the density of the underlying material is doubled and the
daily usage of the equipment is halved, what will be the percentage increase in the useful life of the
equipment?
If m > 0, y > 0, and x is m percent of 2y, then, in terms of y, m is what percent of x?
x% of y is increased by x%. What is the result in terms of x and y?
The manufacturer’s suggested retail price (MSRP) of a certain item is $60. Store A sells the item for 20
percent more than the MSRP. The regular price of the item at Store B is 30 percent more than the MSRP, but
the item is currently on sale for 10 percent less than the regular price. If sales tax is 5 percent of the
purchase price at both stores, what is the result when the total cost of the item at Store B is subtracted from
the total cost of the item at Store A?
Two years ago, Sam put $1,000 into a savings account. At the end of the first year, his account had accrued
$100 in interest bringing his total balance to $1,100. The next year, his account balance increased by 10%. At
the end of the two years, by what percent has Sam's account balance increased from his initial deposit of
$1,000?


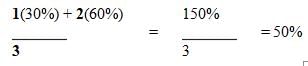

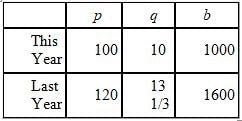
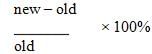
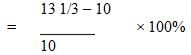
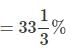

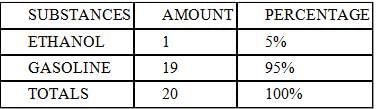
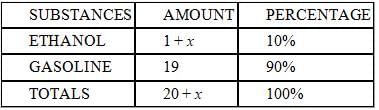
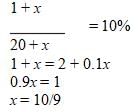
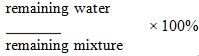
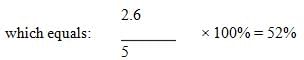
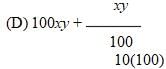
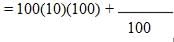 which doesn't equal 11
which doesn't equal 11