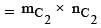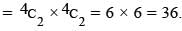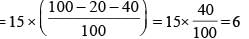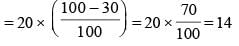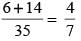Test: Permutation, Combination & Probability - 1 (2019-2017) - UPSC MCQ
10 Questions MCQ Test - Test: Permutation, Combination & Probability - 1 (2019-2017)
The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of four parallel lines, is
[2019]
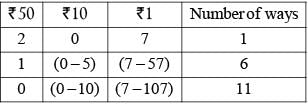
Suppose you have sufficient amount of rupee currency in three denominations: ₹1, ₹10 and ₹ 50. In how many different ways can you pay a bill of ₹ 107?
[2019]
A printer numbers the pages of a book starting with 1 and uses 3089 digits in all. How many pages does the book have?
[2019]
How many triplets (x, y, z) satisfy the equation x + y + z = 6, where x, y and z are natural numbers?
[2019]
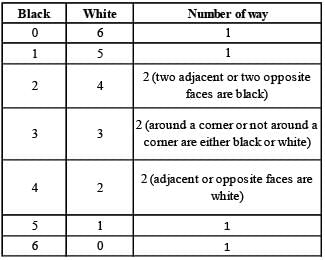
Each face of a cube can be painted in black or white colours. In how many different ways can the cube be painted?
[2019]
A bag contains 15 red balls and 20 black balls. Each ball is numbered either 1or 2 or 3. 20% of the red balls are numbered 1 and 40% of them are numbered 3. Similarly, among the black balls, 45% are numbered 2 and 30% are numbered 3. A boy picks a ball at random. He wins if the ball is red and numbered 3 or if it is black and numbered 1 or 2. What are the chances of his winning?
[2018]
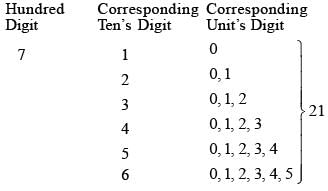
While writing all the numbers from 700 to 1000, how many numbers occur in which the digit at hundred’s place is greater than the digit at ten’s place, and the digit at ten’s place is greater than the digit at unit’s place?
[2018]
How many diagonals can be drawn by joining the vertices of an octagon?
[2018]
For a sports meet, a winners’ stand comprising three wooden blocks is in the following form :
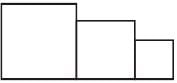
There are six different colours available to choose from and each of the three wooden blocks is to be painted such that no two of them has the same colour. In how many different ways can the winners’ stand be painted?
[2018]
If 2 boys and 2 girls are to be arranged in a row so that the girls are not next to each other, how many possible arrangements are there?
[2017]