Test: Permutation, Combination & Probability - CAT MCQ
10 Questions MCQ Test - Test: Permutation, Combination & Probability
How many numbers with two or more digits can be formed with the digits 1,2,3,4,5,6,7,8,9, so that in every such number, each digit is used at most once and the digits appear in the ascending order?
(2018)
The first n natural numbers, 1 to n, have to be arranged in a row from left to right. The n numbers are arranged such that there are an odd number of numbers between any two even numbers as well as between any two odd numbers. If the number of ways in which this can be done is 72, then find the value of n.
(2016)
If we arrange the letters of the word ‘KAKA’ in all possible ways, what is the probability that vowels will not be together in an arrangement?
(2015)
Three persons - A, B and C - are playing the game of death. 3 bullets are placed randomly in a revolver having 6 chambers. Each one has to shoot himself by pulling the trigger once after which the revolver passes to the next person. This process continues till two of them are dead and the survivor of the game becomes the winner. What is the probability that B is the winner if A starts the game and A, B and C take turns in that order.
(2015)
Amar, Akbar and Antony are three students in a class of 9 students. A class photo is taken. The number of ways in which it can be taken such that no two of Amar, Akbar and Antony are sitting together is:
(2014)
If p is the probability of head turning up in the toss of a coin (not necessarily fair) and q is the probability of a tail turning up. Find the minimum possible value of 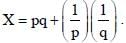
(2014)
There are exactly sixty chairs around a circular table. There are some people sitting on these chairs in such a way that the next person to be seated around the table will have to sit next to someone. What is the least possible number of people sitting around the table currently?
(2014)
In how many ways can 18 identical candies be distributed among 8 children such that the number of candies received by each child is a prime number?
(2013)
What is the probability that the product of two integers chosen at random has the same unit digit as the two integers?
(2012)
A box contains five yellow and five green balls. A ball is picked from the box and is replaced by a ball of the other colour. For instance, if a green ball is picked then it is replaced by a yellow ball and vice-versa. The process is repeated ten times and then a ball is picked from the box. What is the probability that this ball is yellow?
(2011)




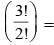 3 arrangements.
3 arrangements.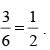
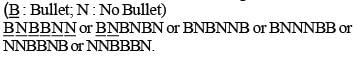
 the
the