Test: Permutation & Combination- 3 - CAT MCQ
15 Questions MCQ Test - Test: Permutation & Combination- 3
The total number of 9-digit numbers which have all different digits is
Find the number of non-negative integral solutions to the system of equations x + y + z + u + t = 20 and x + y + z = 5.
Ateacher takes 3 children from her class to the zoo at a time as often as she can, but she does not take the same three children to the zoo more than once. She finds that she goes to the zoo 84 times more than a particular child goes to the zoo. The number of children in her class is
If x, y, and z are integers and x ≥ 0, y ≥ 1, z ≥ 2, x+y + z= 15 then the number of values of the ordered triplet (x, y, z) is
In an examination, the question paper contains three different sections A, B and C containing 4, 5 and 6 questions respectively. In how many ways, a candidate can make a selection of 7 questions, selecting at least two questions from each section?
The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines, is
A lady gives a dinner party to 5 guests to be selected from nine friends. The number of ways of forming the party of 5, given that two particular friends A and B will not attend the party together is
If a denotes the number of permutations of x + 2 things taking all at a time, b the number of permutations of x things taking 11 at a time and c the number of permutations of x - 11 things taking all at a time such that a = 182be, then the value of x is
How many 10 digits numbers can be written by using the digits 1 and 2
In a room there are 2 green chairs, 3 yellow chairs and 4 blue chairs. In how many ways can Raj choose 3 chairs so that at least one yellow chair is included?
Find the number of non-congruent rectangles that can be found on a chessboard normal 8 x 8 chessboard,
Find the number of integral solutions of equation:
x + y + z + t = 29, when x ≥ 1,y ≥ 2, z ≥ 3 and t ≥ 0 is.
There is a regular decagon. Triangles are formed by joining the vertices of the polygon. What is the number of triangles which have no side common with any of the sides of the polygon?
The number of positive integral solution of abc = 30 is:
A dinner menu is to be designed out of 5 different starters, 6 identical main courses and 4 distinct desserts. In how many ways menu be designed such that there is atleast one of each of the starters, main courses and desserts?



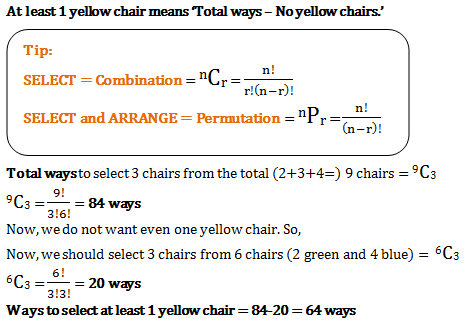

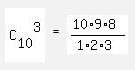 = 10*3*4 = 120.
= 10*3*4 = 120.










